Задачи раздел 1

Задача 1.2 (Цветков) В теплообменнике горячий и холодный теплоносители

разделены плоской латунной стенкой [δ = 2 мм, λ = 100 Вт/(м*К)], перепад температур в которой t_с1 – t_с2 = 5 °C.

Вычислить плотность теплового потока через стенку.

Определить толщину стальной [λ = 45 Вт/(м*К]) и медной [λ = 370 Вт/(м*К)] стенок, чтобы при том же перепаде температур плотность теплового потока осталась неизменной.
Скачать решение задачи 1.2 (Цветков (цена 100р)

---

Задача 1.3 (Цветков) Чему равен тепловой поток через стену из красного кирпича высотой 4 м, шириной 5 м и толщиной 500 мм? На одной поверхности стены температура 19 °С, на другой 2 °С.

Ответ Q = 523,6 Вт
Скачать решение задачи 1.3 (Цветков (цена 100р)

---

Задача 1.4 (Цветков) Чему равен тепловой поток через стену из красного кирпича высотой 4 м, шириной 5 м и толщиной 500 мм? На одной поверхности стены температура 19 °С, на другой 2 °С.

Ответ q = 493,6 Вт/м².
Скачать решение задачи 1.4 (Цветков (цена 100р)

---

Задача 1.5 (Цветков) Плотность теплового потока через плоскую стенку толщиной 200 мм составляет 200 Вт/м², а разность температур ее поверхностей 50 °С. Определить коэффициент температуропроводности стенки, если ρ = 1700 кг/м3, c_р = 0,88 кДж/(кг*К).

Ответ а = 0,535*10-6 м²/с.
Скачать решение задачи 1.5 (Цветков (цена 100р)

---

Задача 1.6 (Цветков) К двум торцам нагревателя цилиндрической формы d = 300 мм плотно прижаты два идентичных образца материала того же диаметра толщиной δ = 5 мм. Определить коэффициент теплопроводности образцов, если при мощности нагревателя Q = 56,5 Вт перепады температур по толщине образцов составили 12,5 °С. Радиальный перенос тепла в системе пренебрежимо мал (рис. 1.1).

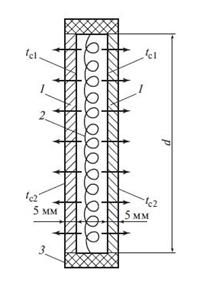
Ответ q = 493,6 Вт/м².

Скачать решение задачи 1.6 (Цветков (цена 100р)

---

Задача 1.7 (Цветков) Дана трехслойная плоская стенка: δ₁ = 20 мм; λ₁ = 20 Вт/(м*К); t_с1 = 10 °С; λ₂ = 5 + 0,05t Вт/(м*К); t_с4 = 60 °С; δ₃ = 60 мм; λ₃ = 10 Вт/(м*К); t_ж2 = 150 °С; α2 = 18 Вт/(м2*К). Найти б2.

Ответ б₂ = 157мм.
Скачать решение задачи 1.7 (Цветков (цена 100р)

---

Задача 1.8 (Цветков) Плоскую поверхность с t_с = 250 °С решено изолировать листовым асбестом, у которого λ = 0,157 + (0,14*10^–3)t Вт/(м*К). Какой толщины должен быть слой изоляции, если допустимая температура наружной ее поверхности 50 °С, а тепловые потери не должны превышать 500 Вт/м²?

Ответ б = 71,2мм.
Скачать решение задачи 1.8 (Цветков (цена 100р)

---

Задача 1.9 (Цветков) Внутренний слой стен топочной камеры парового котла выполнен из шамотного кирпича (δ_ш = 120 мм), наружный слой - из пеношамота (δ_п = 500 мм), плотно прилегающих друг к другу. Температуры на соответствующих поверхностях пеношамота составляют t_с2 = 800 °С и t_с3 = 60 °С. Вычислить температуру на внутренней поверхности слоя из шамотного кирпича с учетом зависимости его коэффициента теплопроводности от температуры (рис. 1.2).

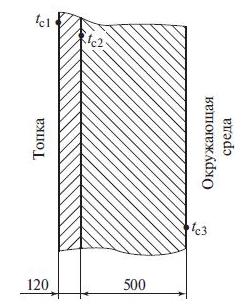
Ответ: t_c1 = 856,3 °С.

Скачать решение задачи 1.9 (Цветков (цена 100р)

---

Задача 1.10 (Цветков) Стены сушильной камеры толщиной 0,256 м, выполненные из слоя красного кирпича [λ_к = 0,71 Вт/(м*К)] и слоя войлока [λ_в = 0,047 Вт/(м*К)], имели температуры t_с1 = 120 °С и t_с3 = 35 °C на внутренней и внешней поверхностях соответственно. Увеличение толщины слоя войлока на 0,028 м снизило тепловые потери вдвое и t_с3 на 10 °С при неизменной t_с1. Определить толщину кирпичного слоя и максимальные температуры войлока в обоих случаях.

Ответ: t_c2 = 155,6 °С бв = 36мм.
Скачать решение задачи 1.10 (Цветков (цена 100р)

---

Задача 1.11 (Цветков) Обмуровка печи состоит из слоев шамотного кирпича [λ_ш = 0,93 Вт/(м*К), δ_ш = 120 мм] и красного кирпича [λ_к = 0,7 Вт/(м*К), δ_к = 250 мм], между которыми засыпка из диатомита [λ_д = 0,13 Вт/(м*К), δ_д = 60 мм]. Какой толщины следует сделать слой засыпки, если толщину слоя из красного кирпича удвоить при условии сохранения плотности теплового потока через обмуровку и температур на внешних ее поверхностях?

Ответ: бд = 11,5мм.
Скачать решение задачи 1.11 (Цветков (цена 100р)

---

Задача 1.12 (Цветков) Плотность теплового потока через плоскую кварцевую стенку [λ = 3 Вт / (м*К), δ = 10 мм] составляет q = 3*10⁴ Вт/м². Со стороны одной из ее поверхностей заданы температура жидкости t_ж = 30 °С и коэффициент теплоотдачи α = 100 Вт/(м²*К). Найти температуры на обеих поверхностях стенки.

Ответ: t_c1 = 430 °С.
Скачать решение задачи 1.12 (Цветков (цена 100р)

---

Задача 1.15 (Цветков) Определить необходимую мощность радиаторов отопления аудитории, если кладка ее наружной стены (L = 8 м, H = 4,5 м, δ = 0,5 м) выполнена из красного кирпича на холодном растворе, а температуры поверхностей t_с1 = 12 °С и t_с2 = –15 °С. (Окна условно отсутствуют.)

Какова глубина промерзания стены?
Как изменится полученный результат с учетом того, что слои штукатурки на внутренней и внешней поверхностях стены δ_ш.вн = δ_ш.вш = 10 мм при других одинаковых условиях, если:
а) штукатурка известковая;
б) штукатурка цементно-песчаная?
Ответ: Q = 1496,9 Вт; Qа = 1433,8 Вт; Qб = 1459,4 Вт; l = 0,278 м; lа = 0,288 м; lб = 0,289 м
Скачать решение задачи 1.13 (Цветков (цена 100р)

---

Задача 1.16 (Цветков) Окно в аудитории имеет сдвоенные рамы с зазором между стеклами 60 мм. Вычислить тепловые потери через оконный проем 3×3 м без учета конвекции в зазоре и теплового излучения, если толщина стекол δ = 4 мм, а температуры их соответствующих поверхностей t_с1 = 12 °С и t_с4 = –15 °С.

Ответ Q = 98,4Вт.
Скачать решение задачи 1.16 (Цветков (цена 100р)

---

Задача 1.35 (Цветков) Для десятикратного увеличения теплового потока с 1 п.м наружной поверхности вертикальной трубы (d = 60 мм, t_c = 80 °С) к воздуху в помещении (tж = 20 °С) решено приварить к ней с равномерным шагом по периметру продольные стальные [λ = 50,1 Вт/(м*К)] ребра прямоугольного сечения толщиной 3 мм. Длина ребер l = 50 мм. Какое число ребер потребуется для этого, если коэффициент теплоотдачи с поверхности трубы и ребер 7,5 Вт/(м²*К)? Чему равен тепловой поток с гладкой части поверхности трубы между ребрами (рис. 1.4)?

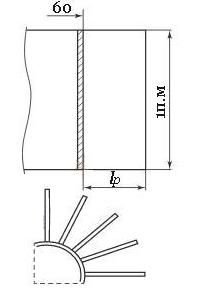
Ответ: Q_p = 41,6 Вт/м, число ребер w = 19шт.

Скачать решение задачи 1.35 (Цветков (цена 150р)

---

Задача 1.36 (Цветков) Конденсатор холодильной машины обдуваемый воздухом, представляет собой змеевик из латунных труб (d₂*б = 8 x 1 мм), на которые плотно насажены алюминиевые ребра - квадратные пластины толщиной б_р = 0,3 мм и стороной b = 60 мм. Центр квадрата совпадает с осью трубы; шаг между ребрами 4 мм. Температура хладагента в конденсаторе t_ж1 = 35 °С; температура воздуха tж2 = 20 °С. Коэффициент теплоотдачи к воздуху а₂ = 50 Вт/(м2*К), а теплоотдача от хладагента а₁ >> а₂. Рассчитать длину труб конденсатора, необходимую для отвода Q = 3,5 кВт (рис. 1.5).

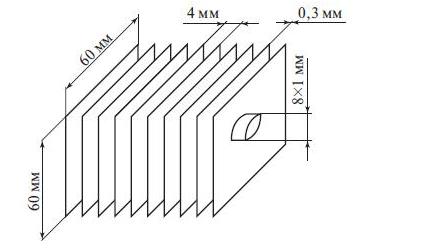
Ответ а₁ = 6,09 м.

Скачать решение задачи 1.36 (Цветков (цена 150р)

---

Задача 1.37 (Цветков) Вычислить тепловой поток с 1 п.м длины стальных труб d₂×δ = 32×5 мм водяного экономайзера парогенератора для двух вариантов: а) экономайзер гладкотрубный; б) наружная поверхность труб с круглыми ребрами, внешний диаметр которых D_р = 58 мм, толщина δ_р = 1,2 мм. Шаг между ребрами s = 4,8 мм. В обоих вариантах средняя температура дымовых газов 450 °С, а воды в трубах 270 °С; коэффициент теплоотдачи от внутренней поверхности труб к воде 5200 Вт/(м²*К). Коэффициент теплоотдачи со стороны дымовых газов: в первом варианте 115 Вт/(м²*К); во втором варианте коэффициент теплоотдачи как на ребрах, так и на гладкой межреберной поверхности трубы составляет 85 Вт/(м²*К) (рис. 1.6).

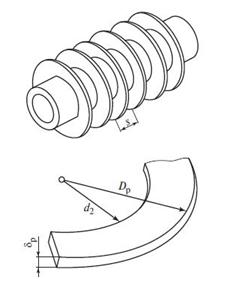
Ответ: Q = 9169 Вт.

Скачать решение задачи 1.37 (Цветков (цена 150р)

---