Часть 10 (Решение задач из сборника Куколевского)
Часть 10-1 Расчет сложных трубопроводов
Задача (Куколевский И.И.) 10-1. Найти как распределяется расход Q = 25 л/с между двумя параллельными трубами, одна из которых имеет длину l1 = 30м, диаметр d1 = 50 мм, а другая (с задвижкой, коэффициент сопротивления которой ξ = 3) имеет длину l2 = 50 м и диаметр d2 = 100 мм.
Какова будет потеря напора hn в разветвленном участке? Значения коэффициентов сопротивления трения труб принять соответственно равными λ1 = 0,04 и λ2 =0,03.
Ответ. Q1= 4,45 л/сек и Q2 = 20,55 л/сек; hn = 6,3м

Скачать решение задачи 10-1 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-2. Смазочное масло (δ = 0,8, v = 6 сСт) подводится к подшипникам коленчатого вала по системе трубок, состоящей из пяти одинаковых участков каждый длиной l = 500 мм и диаметром d = 4 мм.
1) Сколько смазки нужно подать к узловой точке А системы, чтобы каждый подшипник получил ее не менее 8 см3/с?
2) Как изменится потребное количество смазки, если участки АВ заменить трубой диаметром D = 8 мм? Давление на выходе из трубок в подшипники считать одинаковым, местными потерями пренебречь.
Ответ. 1) Q=64 см3/с. 2) Q = 26 см3/с.

Скачать решение задачи 10-2 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-3. Сифонный трубопровод составлен из трех труб, приведенные длины которых L1 = 50 м, L2 = 100 м, L3= 150 м и диаметры d1 = 75 мм, d2 = 50 мм, d3 = 75 мм.
Определить напор Н, необходимый для того, чтобы из резервуара А в резервуар В поступал расход воды Q2 = 3 л/с.
Найти при этом напоре величину наименьшего давления в трубопроводе, если h = 2 м и длина участка CD трубы 3 равна 20 м.
Задачу решить в предположении квадратичной области сопротивления труб, приняв λ1 = 0,025, λ2 = 0,028, λ3 = 0,025. Скоростными напорами пренебречь. Атмосферное давление принять равным 100 кПа.
Ответ. Н= 6,7 м; Pmin = 27,69 кПа.

Скачать решение задачи 10-3 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-4. Резервуары А и В с постоянными и одинаковыми уровнями соединены системой труб, приведенные длины которых L1 = 400 м, L2 = 180 м, L3 = 50 м, L4 = 400 м и диаметры d1 = d2 = d3 = 100 мм, d4 = 200 мм.
1) При каком давлении р над поверхностью воды в резервуаре А расход в трубе 4 будет равен Q4 = 40 л/с?.
2) Каков при этом суммарный расход Q1 воды из резервуара А в резервуар В?
Задачу решить в предположении квадратичной области сопротивления, приняв λ1 = λ2 = λ3 = 0,025; λ4 = 0,02.
Ответ. 1) Р = 3,7 МПа. 2) Q1= 67,3 л/с.

Скачать решение задачи 10-4 (Куколевский И.И.) (цена 100р)
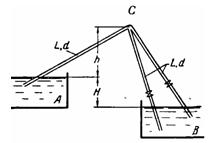
Задача (Куколевский И.И.) 10-5. Определить расход Q воды (v = 0,01 Ст), поступающий под напором H = 5 м из резервуара A в резервуар В по сифонному трубопроводу, состоящему из стальных (Δ = 0,2 мм) труб диаметрами d = 100 мм и длинами L = 100 м.
Какова максимально возможная высота h расположения точки С сифона, если предельно допустимая в этом узле вакууметрическая высота равнв 10м..
Ответ. Q = 14,2 л /сек; h = 6 м.
Скачать решение задачи 10-5 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-6. Соляровое масло подается самотеком из резервуара А в резервуар В по трубопроводу, состоящему из трех одинаковых труб длинами L = 50 м и диаметрами d = 25 мм.
1) Каким должен быть напор Н трубопровода, чтобы при температуре масла t = 10° С в резервуар В поступал расход Q = 0,2 л/с?
2) Как изменится расход при том же напоре, если температура масла повысится до 20°С?
Местные потери в каждой трубе составляют 20% от потерь по длине. Зависимость кинематического коэффициента вязкости масла от температуры задана графиком.
Ответ. 1) H = 5,75 м. 2) Q = 0,6 л/сек.

Скачать решение задачи 10-6 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-7. Два резервуара с постоянными и одинаковыми уровнями воды (v = 0,01 Ст) соединены стальными (шероховатость Δ = 0,2 мм) трубами, длины которых L1 = L3 = 50 м, L2 = 200 м и диаметры d =100 мм.
1) При каком напоре Н суммарный расход из баков равен Q=12 л/с?
2) Какова максимально возможная высота h расположения узла С при этом напоре? Предельную вакууметрическую высоту в этом узле принять 10м
Ответ. 1) Н = 2,07 м 2) h = 11,4 м.

Скачать решение задачи 10-7 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-8. Определить магистральный расход воды в системе труб, соединяющих два резервуара с разностью уровней Н = 24 м, если размеры труб L1 = L2 = L3 = L4 = 100 м, d1 = d2 = d4 = 100м, d3 = 200м. Значения коэффициента сопротивления трения в трубах λ1 = λ2 = λ4 = 0,025, λ3 = 0,02 и коэффициента сопротивления задвижки ξ = 30. Потерями напора в остальных местных сопротивлениях пренебречь.
Как повлияет на величину расхода закрытие задвижки?
Ответ. Q= 23,7 л/с. Q = 19,6 л/ с.

Скачать решение задачи 10-8 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-9. Вода вытекает в атмосферу из бака с постоянным уровнем Н через трубу длиной L = 150 м, диаметром d = 50 мм.
1) При какой длине L1, параллельной ветви того же диаметра расход увеличится на 20%?
2) Какая длина L2 параллельной ветви диаметром d2 = 100 мм обеспечит такое же увеличение расхода?
3) На сколько увеличится расход, если использовать одновременно обе параллельные ветви?
Задачу решить, пренебрегая местными потерями напора и скоростным напором на выходе из трубы. Коэффициенты сопротивления трения считать постоянными и одинаковыми для всех труб.
Ответ. 1) L1 = 60,9 м. 2) L2 = 46,4 м. 3) на 25%.

Скачать решение задачи 10-9 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-10. Емкость, вместимостью 20 м3 должна наполняться водой (v = 0,01 Ст) в течение 10 мин из крана К, соединенного с водонапорной башней трубопроводом длиной L1 = 800 м.
1) Определить диаметр d1 этого трубопровода, если напор в башне Н = 20 м и кран соединен с тендером трубой длиной l2 = 20 м и диаметром d2 = d1.
2) Как повлияет на время заполнения тендера присоединение второго крана с трубой L3 = 80 м d3 = d1?
Трубопроводы стальные с шероховатостью Δ = 0,2 м. Местными потерями и скоростными напорами на выходе из труб пренебречь.
Ответ. 1) d1 = 152 мм. 2) t = 14,8 мин.

Скачать решение задачи 10-10 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-11. Определить расходы Q1 и Q2 воды (v = 0,01 Ст), поступающей под напором H = 3,6 м из резервуара в пункты 1 и 2 с атмосферным давлением по трубопроводам (Δ = 0,02) диаметрами d = d1 = 60 мм, d2 = 50 мм и длинами L = 60 м, L1 = 30 м, L2 = 25 м.
Вычислить максимально возможную высоту h расположения точки С при предельной вакууметрической высоте, равной 10 м.
Ответ. Q1 = 2,8 л/с; Q2 = 2 л/сек; h = 10,72 м.

Скачать решение задачи 10-11 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-12. По двум последовательно соединенным стальным трубопроводам (Δ = 0,2 мм) длинами L1 = L2 = 400 м и диаметрами d1 = 40 мм, d2 = 60 мм из бака A в бак В самотеком поступает вода (v = 0,01 Ст).
1. Определить расход Q воды при разности уровней в баках H = 20 м.
2 Как изменится расход, если к одному из трубопроводов присоединить параллельную ветвь той же длины и того же диаметра?
Местными сопротивлениями пренебречь.
Ответ. 1) Q= 1,38 л/с; 2) Q = 2,38 л/с; Q = 1,43 л/с.

Скачать решение задачи 10-12 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-13. Питание резервуаров A и В с постоянными и одинаковыми отметками уровней Δ5 осуществляется подачей воды из магистрального трубопровода L1 = 40 м; d1 = 80 мм в распределительные трубы L2 = L3 = 80 м и d2 = d3 = 50 мм,
1 Определить расходы, поступающие в резервуары, если давление в магистральном трубопроводе на уровне нулевой отметки М = 0,49 МПа.
2 Как изменится расход в магистральном трубопроводе, если одну из распределительных труб выключить?
3 Какова в обоих случаях наибольшая возможная высота h расположения распределительных труб относительно уровня воды в резервуарах?
Заглублением труб под уровнями воды в резервуарах пренебречь и считать участки этих труб от сечений С расположенными вертикально. Предельную вакууметрическую высоту в этих сечениях принять равной 10 м. Значения коэффициентов сопротивления трения в трубах принять λ1 = 0,025, λ2 = λ3 = 0,03 и коэффициенты сопротивления задвижек ζ = 3.
Ответ. 1) Q2 = Q3 = 7,5 л/с 2) Q = 8 л/с. 3) h1 = 23 м; h2 = 26 м.

Скачать решение задачи 10-13 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-14. Из резервуаров А и В с одинаковыми уровнями вода по трубам (L1 = 200 м, d1 = 200 м и L2 = 100 м, d2 = 100 мм) поступает в магистральную трубу длиной L3 = 600 м, диаметром d3 = 200 мм, а затем сливается в резервуар С.
1 Определить расход Q3, поступающий в резервуар С при напоре H = 16 м и коэффициенте сопротивления задвижки ξ = 12.
2 Чему равен (при том же напоре Н) минимальный коэффициент сопротивления задвижки, если минимальное абсолютное давление в системе принять равным нулю?
Длина горизонтального участка трубы 3 равна 160м, высота его расположения над уровнем моря h = 4 м. Принять λ1 = λ3 = 0,02 и λ2 = 0,025. Кроме потерь в задвижке, другие местные потери напора не учитывать. Атмосферное давление принять равным 98 кПа
Ответ. 1) Q = 60,22 л/с. 2) ξmin = 9,4.

Скачать решение задачи 10-14 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-15. Трубопровод диаметром D и длиной L заменяется двумя одинаковыми параллельными трубами той же длины, суммарная площадь которых равна площади сечения трубопровода.
Определить, как изменится при постоянном напоре пропускная способность системы при следующих законах сопротивления: 1) ламинарном; 2) гидравлически гладких труб (формула 9-16 гл. 9); 3) квадратичном (формула 9-20 гл. 9).
Ответ.Q2/Q1= 0,5; Q2/Q1 = 0,78; Q2/Q1 = 0,8.
Скачать решение задачи 10-15 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-16. Для увеличения пропускной способности трубопровода длиной 2L и диаметром А к нему присоединена параллельная ветвь того же диаметра и длиной L (пунктир). Определить, какова эквивалентная длина разветвленного участка и во сколько раз увеличится расход при неизменном напоре для следующих законов сопротивления: 1) ламинарного; 2) гидравлически гладких труб (формула 9-16 гл. 9); 3) квадратичного (формула 9-20 гл. 9).

Ответ: 1) L2 = L/2, Q2/Q1 = 1,33; 2) L2 = L/3,36; Q2/Q1 = 1,28; 3) L2 = L/4; Q2/Q1 = 1,265.
Скачать решение задачи 10-16 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-17. Определить высоту Н уровня воды в резервуаре, при которой для изображенного на схеме трубопровода в случае отбора из узловой точки А расхода QА = 35 л/с в концевом сечении (где давление равно атмосферному) расход будет QB = 50 л/с. Длины, диаметры и коэффициенты трения для ветвей трубопровода следующие;
L1 = 300 м; d1 = 225 мм; λ1 =0,030;
L2 = 150 м;d2 = 125 мм; λ2 = 0,038;
L3 = 250 м; d3 = 150 мм; λ3 = 0,032;
L4 = 100 м; d4 = 175 мм; λ4 = 0,042.
Найти величину у напора в узловой точке А системы.
Ответ. Н = 21,7 м; у = 12,4 м
 .
.
Скачать решение задачи 10-17 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-18. По магистральному трубопроводу длиной L = 1000 м и диаметром D = 200 мм протекает транзитный расход воды Qт = 40 л/с. По длине, трубопровода в точках, расположенных на равных расстояниях l = 50 м, из него отбираются равные расходы q = 2 л/с.
1 Определить сопротивление h трубопровода, учитывая только потери на трение при λ = 0,025.
2 Как изменится сопротивление трубопровода, если весь расход, идущий через его начальное сечение (равный 80 л/с):
а) пропустить через трубопровод транзитно, не отбирая его по длине;
б) отбирать по длине трубопровода при Q = 4 л/с и равном нулю транзитном расходе. Указание. При достаточно большом числе точек отбора можно применить формулу для непрерывной раздачи.
Ответ. 1) h = 24,1 м. 2) hа = 41,4 м; hб = 13,8 м.

Скачать решение задачи 10-18 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-19. Трубопровод диаметром d = 125 мм и общей длиной 2L = 400 м соединяет два резервуара с постоянной разностью уровней воды H = 20 м.
1 При каком расходе Q, отбираемом из трубопровода в середине его длины, поступление воды в нижний резервуар прекратитс?
2. Какие расходы установятся в левой и правой ветвях трубопровода при значениях отбираемого расхода Q, вдвое большем и вдвое меньшем найденного выше?
Учитывать только потери на трение, принимая λ = 0,025.
Ответ. Q = 38,4 л/с. При Q = 76,8 л/сек расход из верхнего резервуара Q1 = 48 л/с и в нижний резервуар Q2 = 28,8 л/с. При Q = 50,8 л/с расход из нижнего резервуара Q2 = 15,8 л/сек и их верхнего Q1 = 35 л/сек.

Скачать решение задачи 10-19 (Куколевский И.И.) (цена 100р)
Часть 10-2 Расчет сложных трубопроводов
Задача (Куколевский И.И.) 10-20. Перемещение поршня гидроцилиндра (D1 = 150 мм, D2 = 50 мм), нагруженного внешним усилием R = 200 H, осуществляется подачей спиртоглицериновой смеси (v = 1 Ст, ρ = 1245 кг/м3) насосом в рабочую полость гидроцилиндра.
Для регулирования скорости перемещения поршня при постоянной подаче насоса служит кран К на сбросной трубе, присоединенной к узлу А системы.
1) Какова скорость V перемещения поршня, если подача насоса Q = 7,85 л/с, приведенные длины труб L1 = 5 м, L2 = 10 м, диаметр труб d = 50 мм.
2) Какова максимальная скорость vмакс при той же подаче насоса;
3) При какой наименьшей приведенной длине сбросной трубы (при открытии крана К) перемещение поршня прекратится?
Ответ. 1) v = 0,36 м/с. 2) vmax = 0,83 м/сек, 3) L2min = 2,5 м.

Скачать решение задачи 10-20 (Куколевский И.И.) (цена 100р)
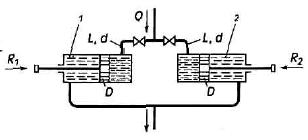
Задача (Куколевский И.И.) 10-21. Перемещение поршней гидроцилиндров диаметра D = 15 см, нагруженных внешними силами R1 = 1000 H и R2 = 2000 H, осуществляется подачей спиртоглицериновой смеси (v = 1 Ст, ρ = 1220 кг/м3} по трубам одинаковой приведенной длины L = 10 м и диаметра d = 4 см в гидроцилиндры 1 и 2.
1 Определить скорости перемещения поршней при расходе Q = 7 л/с в магистрали.
2 Какое дополнительное сопротивление (выраженное эквивалентной длиной) и в какой трубе нужно создать, чтобы при том же расходе в магистрали скорости поршней стали одинаковыми?
Сопротивлением сливной линии пренебречь, считая давление в нерабочих полостях атмосферным.
Ответ. 1) v1 = 0,28 м/сек; v2 = 0,117 м/сек, 2) L2 = 8,2 м на первой трубе
Скачать решение задачи 10-21 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-22. Шестеренный насос с подачей Q = 4 л/с засасывает бензин из двух баков с начальной разностью уровней h = 0,5 м по трубам одинакового диаметра d = 50 мм и одиннаковой длины до узловой точки L = 10 м.
Определить начальный расход из верхнего QB и нижнего QH баков.
Указать, при какой разности уровней h начальный расход из нижнего бака будет равен нулю.
Определить, на какой глубине z под дном нижнего бака следует расположить узловую точку системы, чтобы после опорожнения верхнего бака было исключено попадание воздуха в насос и нижний бак можно было опорожнить до конца.
Учитывать только потери на трение, приняв λ = 0,02.
Ответ. Qв = 3,18 л/сек; Qн = 0,82 л/сек; h = 0,85 м: z = 0,85 м.

Скачать решение задачи 10-22 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-23. Найти, как распределится расход Q1 = 10 л/сек воды (v = 0,01 Ст) между двумя стальными трубами (Δ = 0,2 мм), длины которых L2 = 31,2 м, L3 = 71,2 м и диаметры d2 = d3 = 0,05 м, если высоты расположения их выходных сечений H2 = 4 м и Н3 = 10 м а суммарный коэффициент местных сопротивлений каждой трубы ξ = 5.
Какое избыточное давление р в магистральном трубопроводе обеспечит указанный суммарный расход, если размеры подводящей трубы L1 = 40 м, d1 = 0,075 м нее шероховатость Δ = 0,2 мм?
Как нужно изменить диаметры d2 и d3, чтобы при том же давлении в магистрали расходы в трубах стали равными Q2 =Q3 = 5 л/сек.
Ответ. 1) р = 210 кПа. 2) d2 = 43 мм, d3 = 54 мм.

Скачать решение задачи 10-23 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-24. Баки А, В и С соединены трубопроводами L1 = 75 мм, d1 = 75мм, и L2 = L3 = 100м, d2 = d3 = 50 мм. Напор Н = 10 м.
При каком давлении М на поверхности воды в баке А в бак В будет поступать расход Q2 = 5 л/с?
Как нужно изменить давление М, чтобы вода не поступала в бак В?
Коэффициенты сопротивления трения во всех трубопроводах принять равными λ = 0,03, коэффициент сопротивления задвижки ξ =15
Ответ. М = 279 кПа., M'= 7,75 кПа.

Скачать решение задачи 10-24 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-25. По двум одинаковым, открытым в атмосферу стальным (Δ = 0,2 мм) трубам длинами L2 = L3 = 25 м и диаметрами d2 = d3 = 50 мм требуется подавать одинаковые расходы Q = 5 л/с воды (v = 0,01 Ст) при напорах H = 10 м, h = 7 м.
1 Определить необходимый для этого диаметр d1 стальной трубы, длина которой L1 = 50 м, а также необходимую величину ξ коэффициента сопротивления вентиля, установленного на трубе 3.
2 Какой расход Q' пойдет по трубопроводу и какое давление будет в точке К, если полностью закрыть вентиль на трубе 3.
Ответ. 1) d1 = 85 мм; ξ = 9,1. 2) Q' = 5,75 л/с; Pk = 60 кПа.

Скачать решение задачи 10-25 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-26. Резервуар А с постоянным уровнем Н = 3 м, и избыточным давлением на поверхност M = 0,4 МПа питает водонапорную башню В и бассейн С по системе, состоящей из трех одинаковых труб, приведенной длиной L = 210 м и диаметром d = 100мм каждая.
Определить расход QС, поступающий в бассейн С, и высоту h, на которой установится уровень воды в водонапорной башне, если из нее отводится расход Qв = 5 л/с. Коэффициент сопротивления трения для потоков в трубах принять равным λ = 0,025.
Ответ. Qс = 19,7 л/с; h = 15,8 м.

Скачать решение задачи 10-26 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-27. Определить расходы Q1, Q2 и Q3, воды (v = 0,01 Ст) в стальных (Δ = 0,2 мм) трубах, имеющих длины L1 = 200 м, L2 = 100м и L3 = 150 м и диаметры d1 = d3 = 100 мм, d2 = 80 мм, если напоры H1 = 7 м и H3 = 3 м.
При какой приведенной длине L3' трубопровода 3 расход Q2 станет равным нулю?
Ответ.Q1 = 10,15 л/с; Q2 = 4,10 л/с. Q3 = 14,25 л/с; L3 = 467 м.

Скачать решение задачи 10-27 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-28. Вода вытекает в атмосферу через два одинаковых сходящихся насадка (dн = 20 мм, εн = 1, ξн = 0,06), расположенных ниже уровня питающего их бака на H1 = 12 м и H2 = 18 м.
1 Определить расходы через насадки и теоретические высоты полета струй z1, и z2, если длины труб, соединяющих бак с насадками, равны L = 50 м, L1 = 25 м, а диаметры их одинаковы (d = 50 мм).
2 Каков должен быть коэффициент ξ сопротивления вентиля, обеспечивающий одинаковую высоту полета струй?
Принять коэффициент сопротивления трения труб равным λ = 0,025. При решении первого вопроса местные потери учитывать только в насадках.
Ответ. 1) Q1 = 2,06 л/с; Q2 = 3,20 л/с; z1 = 2,19 м, z2 = 5,26 м. 2) ξ = 64,2.

Скачать решение задачи 10-28 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-29. Из бака А с постоянным уровнем вода поступает в баки В и С по одинаковым трубам L = 100 м, d = 50 мм (λ = 0,03). Из бака В вода вытекает в атмосферу через сходящийся насадок диаметрами dн = 25 мм (ξ = 0,04, ε = 1) при постоянном напоре z.
Определить расходы в каждой из труб при напорах H1 = 15 м и H2 = 10 м и полностью открытых кранах (ξ = 0).
Какими станут расходы и напор z, если полностью закрыть кран на трубе, ведущей в бак С?
Ответ. QA = 3,44 л/с; QВ = 0,78 л/с; Qс = 2,66 л/с; z = 0,134 м.
При закрытом кране Q'А=2,22 л/с; z' = 1,09 м.

Скачать решение задачи 10-29 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-30. Три одинаковых цилиндра диаметром D = 50 мм заполнены маслом (δ = 0,88, v = 0,3 Ст) и соединены трубами L1 = L2 = 22,5 м, L3 = 20 м и d = 25 мм. На поверхностях масла в цилиндрах помещены поршни, нагруженные силами Р1 = 700 Н, Р2 = 640 Н, Р3 = 500 Н.
Определить направления и величины скоростей перемещения поршней.
Пренебречь высотами расположения поршней относительно узловой точки системы, трением в цилиндрах и местными потерями напора в трубах.
Ответ, v1 = 0,374 м/с; v2 = 0,121 м/с; v3 =0,495 м/с.

Скачать решение задачи 10-30 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-31. Из трех резервуаров с одинаковыми уровнями H = 10 м, по одинаковым трубам (L = 50 м, d = 100 мм, λ = 0,025) вода поступает в магистральный трубопровод, состоящий из трех одинаковых участков (L1 = 80 м, d1 = 200 мм λ = 0,021).
1 Определить расход, вытекающий из магистрального трубопровода в атмосферу при полностью открытых задвижках (ξ = 0).
2 Найти расходы Q1, Q2 и Q3, поступающие при этом из резервуаров в магистральный трубопровод.
Ответ. 1) Q = 76,5 л/с, Q1 = 24,8 л/с; Q2 = 25,3 л/с; Q3 = 26,4 л /с.

Скачать решение задачи 10-31 (Куколевский И.И.) (цена 100р)
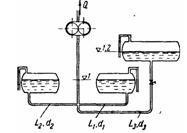
Задача (Куколевский И.И.) 10-32. Определить расход Q1 который подается в верхний бак, если система (L1 = 150 м, d =100 мм, все остальные трубы Li = 50 м, di = 60 мм) работает при постоянных напорах H = 6 м и h = 2 м.
Коэффициент сопротивления трения первой трубы принять равным λ1 = 0,02, а всех остальных труб λ = 0,03, местными потерями пренебречь.
Определить расходы, которые установятся при этом во всех трубах системы.
Ответ. Q1 = 8,76 л/с; Q2 = 5,65 л/с; Q3 = 3,09 л/с; Q4 = 3,11 л/с; Q5 = 2,56 л/с; Q6 = 3,09 л/с.

Скачать решение задачи 10-32 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-33. В три квартиры, расположенные на разных этажах (H = 3,5 м), вода подводится из магистрального трубопровода по вертикальной трубе и горизонтальным отводам, размеры которых L = 4 м, d = 60 мм.
Определить давление в магистрали (показание манометра М), необходимое для того, чтобы расход, подаваемый в любую квартиру при полностью открытых кранах, был не меньше 3 л/с.
Коэффициент сопротивления трения труб принять равным λ = 0,03, а коэффициент сопротивления полностью открытого крана (с угольником) ξ = 3; потери в тройниках не учитывать.
Ответ. M = 262 кПа.

Скачать решение задачи 10-33 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10-34. Насос, подача которого Q = 0,25 л/сек, всасывает бензин одновременно из трех баков по трубам одинакового диаметра d = 10 мм и приведенных длин L1 = 3,6 м, L2 = 4,7 м, L3 = 3 м.
1 Определить при указанных на схеме отметках уровней в баках (отметки даны в метраз) расходы в трубах, приняв коэффициент сопротивления трения равным λ = 0,035.
2 При какой подаче насоса всасывание из нижних баков прекратится?
Ответ. 1) Q3 = 0.13 л/с: Q2 = 0.114 л/с; Q1 = 0.064 л/с. 2) Q = 0.048 л/с.
Скачать решение задачи 10-34 (Куколевский И.И.) (цена 100р)
Часть 10-3 Расчет сложных трубопроводов
Задача (Куколевский И.И.) 10.35. Определить расходы Q1, Q2 и Q3 масла (δ = 0,88, v = 0,5 Ст) в трубах, имеющих длины L1 = L2 = L3 = 15 м и диаметры d1 = d2 = 20 мм, d3 = 15 мм, если статический напор в баках h = 10 м и к поршню гидроцилиндра, диаметр которого D = 60 мм, Приложена сила Р = 1000 Н. Местными потерями напора в трубах, утечками и трением в гидроцилиндре пренебречь.
Ответ. Q1 = 0,91 л/с; Q2 = 0,69 л/с: Q3 = 0,22 л/с.

Скачать решение задачи 10-35 (Куколевский И.И.) (цена 100р)
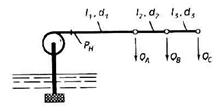
Задача (Куколевский И.И.) 10.36. Определить, какое давление нагнетания рн должен создавать насос, перекачивающий воду по горизонтальному трубопроводу, состоящему из трех последовательных участков размерами l1 = 400 м, d1 = 200 мм; l2 = 200 м, d2 = 150 мм; l3 = 200 м, d3 = 100 мм, если в конечных сечениях участков из трубопровода отбираются одинаковые расходы QA = QC = 10 л/с и минимальный пьезометрический напор в конце трубопровода должен равняться Нс = 5м столба воды. Все участки трубопровода имеют одинаковую шероховатость Δ = 0,5 мм.
Ответ. Pи = 142 кПа.
Скачать решение задачи 10-36 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10.37. Поршень гидравлического цилиндра, имеющий диаметр D = 60 мм и нагруженный внешней силой Р = 2250 Н, перемещается под давлением масла (δ = 0,815, v = 0,5 Ст), поступающего в цилиндр из пневмогидравлического аккумулятора по магистральной трубе (l = 20 м, d = 15 мм).
1) Определить, при каком коэффициенте сопротивления ξ дросселя на сливной трубе (диаметром d = 15 мм), присоединенной к магистрали в середине ее длины, скорость поршня будет vn = 0,2 м/с, если избыточное давление в аккумуляторе P0 = 1,35 МПа. Разностью высот расположения агрегатов системы и местными потерями напора в магистральной трубе пренебречь. В сливной трубе учитывать только сопротивление дросселя.
2) Какова будет скорость поршня, если полностью закрыть дроссель на сливной трубе?
3) При каком минимальном значении ξ дросселя поршень остановится?
Ответ. 1) ξ = 239,4.2. 2) vn = 0,3 м/с, 3) ξ = 21,4.

Скачать решение задачи 10-37 (Куколевский И.И.) (цена 100р)
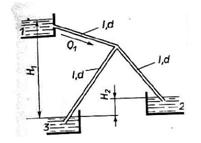
Задача (Куколевский И.И.) 10.38. Резервуары 1, 2 и 3 соединены одинаковыми стальными трубами длиной l = 8 м, диаметром d = 20 мм и шероховатостью Δ = 0,1 мм.
Определить напор воды H1 в резервуаре 1 и расходы воды, поступающие в резервуары 2 и 3, если разность напоров в этих резервуарах Н2 = 3 м и расход в трубе 1 Q1 = 1,2 л/с. Местными потерями напора пренебречь.
Ответ. Н1 = 12,64 м; Q2 = 0,4 л/с; Q3 = 0,8 л/с.
Скачать решение задачи 10-38 (Куколевский И.И.) (цена 100р)
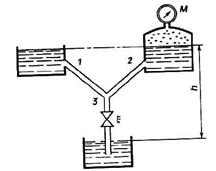
Задача (Куколевский И.И.) 10.39. Определить коэффициент сопротивления ξ, вентиля, при котором расход воды в трубе 3 будет Q3 = 9 л/с, если трубы 1, 2 и 3 имеют одинаковые длины L1 = L2 = L3 = 9м и диаметры d1 = d2 = d3 = 50 мм (λ = 0,025), высота уровней в резервуарах h = 15 м и избыточное давление М = 15 кПа. Учитывать только потери напора на трение по длине труб и потерю напора в вентиле.
Указание. В данной задаче нельзя определить направление потока в трубе 1 методом ее выключения, поскольку неизвестно сопротивление трубы 3. Следует использовать метод нулевого расхода, т.е. предположить, что при совместной работе всех трех груб расход в трубе l равен нулю и напор в узле равен напору в резервуаре I. При этом вычисляется расход Q2 сравнение этого расхода с требуемым расходом позволяет установить направление потока в трубе 1.
Ответ. ξ = 9.
Скачать решение задачи 10-39 (Куколевский И.И.) (цена 100р)
Задача (Куколевский И.И.) 10.40. Найти, как распределится по ветвям кольцевого участка трубопровода расход Q1 = 7500 л/мин, подводимый к участку в узле 1, если известно, что из других узлов отбираются расходы Q3 = 750, Q4 = Q5 = 1500 и Q6 = 3750 л/мин. Размеры ветвей, составляющих кольцевой участок трубопровода:
L12 = 335 м; d12 = 250 мм;
L14 = 245м; d14 = 250мм;
L25 = 245м; d25 = 200 мм;
L45 = 330м; d45 = 200 мм;
L23 = 330м; d23 = 200мм;
L56 = 330 м; d56 = 150 мм;
L36 = 250 м; d36 = 200 мм,
Указать максимальный перепад напоров ΔH между входным узлом 1 и одним из других узлов кольцевого участка. При расчете принять коэффициенты сопротивления трения всех труб равными λ = 0,03.
Ответ. Q14 = 3430 л/мин; Q12 = 4070 л/мин; Q45 = 1930 л/мин; Q25 = 1210 л/мин; Q23 = 2860 л/мин; Q56 = 1640 л/мин; Q36 = 2110 л/мин; ΔH = 12,5 м.

Задача (Куколевский И.И.) 10.41. Трубы, составляющие кольцевой разветвленный участок, имеют следующие размеры:
LAS = 300 м; dAS = 75 мм;
LAK = 250м; dAK = 100 мм;
LKB = 100 м; dKB = 75 мм;
LSB = 265м; dSB=100мм;
LKS= 100м; dKS = 75 мм.
Перепад напоров в узлах A и B участка HAB = 12 м. Определить расходы в трубах и потери напора в них, принимая коэффициент сопротивления трения в трубах λ = 0,032.
Ответ, QAК= 10 л/с; hAK = 6,6 м; QAS = 4,8 л/с; hAS = 7,6 м; QKS = 3,0 л/с; hKS = 1.0 м; QSB = 7,8 л/с; hSB = 4,3 м; QKB = 6,9 л/с; hKB = 5,4 м.

Задача (Куколевский И.И.) 10.42. Определить направления движения и расходы на участках АК, КМ и МВ трубопровода, соединяющего резервуары, разность уровней воды в которых Н = 23 м, если в узлах К и М из трубопровода отбираются одинаковые расходы QК = QМ = 10 л/с и участки имеют одинаковые размеры l = 100м, d = 100 мм. Учитывать только потери на трение по длине (коэффициент сопротивления трения λ = 0,02
Указание. Предварительно нужно определять направление движения на учвстке МВ, предположив, что при заданных отборах в узлах К и М участок выкпючен, и Определив при этом перепад напоров Н в резервуаре А и узле М. Если окажется, что перепад dH > H, то резервуар В является питателем трубопровода, если dH<H то - приемником.
Ответ. QAK= 30л/с; QKM = 20л/с; QMB=10л/с.



