Задачи из задачника Некрасова Б.Б
1 Гидростатика часть 1
Задача 1.1. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 °С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина 20 °С. Модуль объемной упругости бензина принять равным К=1300 МПа, коэффициент температурного расширения 8*104 1/град.
Ответ ΔР = 31,2 МПа
Скачать решение задачи 1.1 из Некрасова Б.Б (цена 60р)
Задача 1.2. Определить избыточное давление на дне океана, глубина которого Н=10 км, приняв плотность морской воды р = 1030 кг/м3 и считая ее несжимаемой. Определить плотность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости К=2*103 МПа.
Ответ Р = 101 МПа, ρ = 1080 кг/м3.
Скачать решение задачи 1.2 из Некрасова Б.Б (цена 60р)
Задача 1.3 Найти закон изменения давления р атмосферного воздуха по высоте z, считая зависимость его плотности от давления изотермической. В действительности до высоты z=11 км температура воздуха падает по линейному закону, т. е. Т = То –b*z, где β = 6,5 град/км. Определить зависимость p = f(z) с учетом действительного изменения температуры воздуха с высотой.
Скачать решение задачи 1.3 из Некрасова Б.Б (цена 60р)
Задача 1.4. Определить избыточное давление воды в трубе В, если показание манометра Рм = 0,025 МПа. Соединительная трубка заполнена водой и воздухом, как показано на схеме, причем H1=0,5 м; H2 = 3 м. Как изменится показание манометра, если при том же давлении в трубе всю соединительную трубку заполнить водой (воздух выпустить через кран K)? Высота H3 = 5 м.
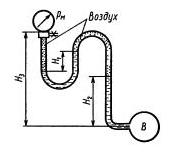
Ответ Рв = 0,05 МПа, Рм = 0.
Скачать решение задачи 1.4 из Некрасова Б.Б (цена 60р)
Задача 1.5. В U-образную трубку налиты вода и бензин. Определить плотность бензина, если hб = 500 мм; hв = 350 мм. Капиллярный эффект не учитывать.
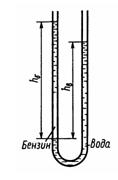
Ответ ρб = 700 кг/м3.
Скачать решение задачи 1.5 из Некрасова Б.Б (цена 60р)
Задача 1.6. В цилиндрический бак диаметром D = 2 м до уровня H = 1,5 м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h = 300 мм. Определить вес находящегося в баке бензина, если рб = 700 кг/м3.
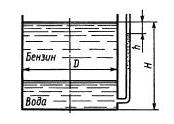
Ответ Gб = 22 кН.
Скачать решение задачи 1.6 из Некрасова Б.Б (цена 60р)
Задача 1.7. Определить абсолютное давление воздуха в сосуде, если показание ртутного прибора h = 368 мм, высота Н = 1 м. Плотность ртути р = 13600 кг/м3. Атмосферное давление 736 мм рт. ст.
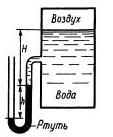
Ответ Рабс = 0,04 МПа.
Скачать решение задачи 1.7 из Некрасова Б.Б (цена 60р)
Задача 1.8. Определить избыточное давление pо воздуха в напорном баке по показанию манометра, составленного из двух U-образных трубок с ртутью. Соединительные трубки заполнены водой. Отметки уровней даны в метрах. Какой высоты Н должен быть пьезометр для измерения того же давления ро? Плотность ртути р = 13 600 кг/м3.
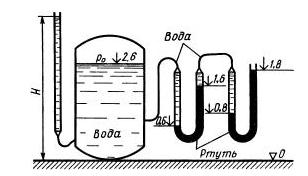
Ответ: Р0 = 0,24 МПа, Н = 27м.
Скачать решение задачи 1.8 из Некрасова Б.Б (цена 60р)
Задача 1.9. Определить силу давления жидкости (воды) на крышку люка диаметром D = 1 м в следующих двух случаях: 1) показание манометра рм = 0,08 МПа; H0=1,5 м; 2) показание ртутного вакуумметра h = 73,5 мм при а = 1 м; pрт= 13600 кг/м3; H0=1,5 м.
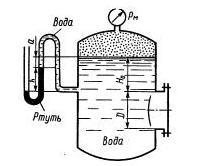
Ответ: F1 = 78 кН, F2 = 0.
Скачать решение задачи 1.9 из Некрасова Б.Б (цена 60р)
Задача 1.10. Определить объемный модуль упругости жидкости, если под действием груза А массой 250 кг поршень прошел расстояние h = 5 мм. Начальная высота положения поршня (без груза) H = 1,5 м, диаметры поршня d = 80 мм и резервуара D = 300 мм, высота резервуара h = 1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким.
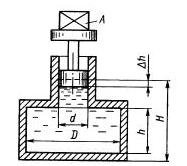
Ответ: К = 1804 МПа.
Скачать решение задачи 1.10 из Некрасова Б.Б (цена 60р)
Задача 1.11 Для опрессовки водой подземного трубопровода (проверки герметичности) применяется ручной поршневой насос. Определить объем воды (модуль упругости К = 2000 МПа), который нужно накачать в трубопровод для повышения избыточного давления в нем от 0 до 1,0 МПа. Считать трубопровод абсолютно жестким. Размеры трубопровода: длина L = 500 м, диаметр d=100 мм. Чему равно усилие на рукоятке насоса в последний момент опрессовки, если диаметр поршня насоса dn = 40 мм, а соотношение плеч рычажного механизма а/b = 5?
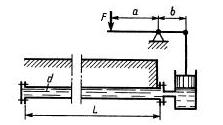
Ответ: ΔV = 1,96л, F = 251 H.
Скачать решение задачи 1.11 из Некрасова Б.Б (цена 60р)
Задача 1.12. Определить абсолютное давление воздуха в баке р1, если при атмосферном давлении, соответствующем ha = 760 мм рт. ст., показание ртутного вакуумметра hрт = 0,2 м, высота h =1,5 м. Каково при этом показание пружинного вакуумметра? Плотность ртути р = 13600 кг/м3.
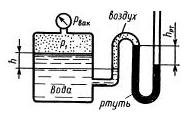
Ответ: Р1 = 0,06 МПа, Рвак = 0,041 МПа.
Скачать решение задачи 1.12 из Некрасова Б.Б (цена 60р)
Задача 1.13. При перекрытом кране трубопровода К определить абсолютное давление в резервуаре, зарытом на глубине H = 5 м, если показание вакуумметра, установленного на высоте h = 1,7 м, равно рвак = 0,02 МПа. Атмосферное давление соответствует hа = 740 мм рт. ст. Плотность бензина рб = 700 кг/м3.
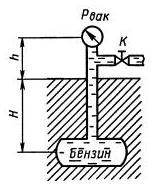
Ответ Р = 0,125 МПа
Скачать решение задачи 1.13 из Некрасова Б.Б (цена 60р)
Задача 1.14. Определить значение силы, действующей на перегородку, которая разделяет бак, если ее диаметр D = 0,5 м, показания вакуумметра рвак = 0,08 МПа и манометра pм = 0,1 МПа.
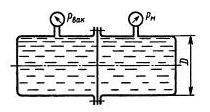
Ответ: F = 35,3 кН.
Скачать решение задачи 1.14 из Некрасова Б.Б (цена 60р)
Задача 1.15. Определить силу, действующую на болты 1 крышки бака, если показание манометра рм=2 МПа, а угол наклона крышки α = 45°. В сечении бак имеет форму квадрата со стороной а = 200 мм.
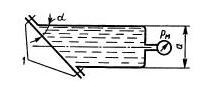
Ответ: F = 113 кН.
Скачать решение задачи 1.15 из Некрасова Б.Б (цена 60р)
Задача 1.16. Определить давление в гидросистеме и вес груза G, лежащего на поршне 2, если для его подъема к поршню 1 приложена сила F = 1 кН. Диаметры поршней: D = 300 мм, d = 80 мм. Разностью высот пренебречь.
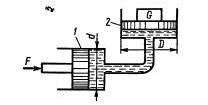
Ответ: Р = 0,199 МПа, G = 14,1 кН.
Скачать решение задачи 1.16 из Некрасова Б.Б (цена 60р)
Задача 1.17. Определить максимальную высоту Hmах, на которую можно подсасывать бензин поршневым насосом, если давление его насыщенных паров составляет hнп = 200 мм рт. ст., а атмосферное давление ha = 700 мм рт. ст. Чему равна при этом сила вдоль штока, если H0 = 1 м, рб = 700 кг/м3; D = 50 мм?
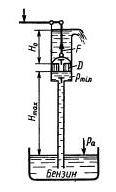
Ответ: Нmax = 9,71м, F = 144 Н.
Скачать решение задачи 1.17 из Некрасова Б.Б (цена 60р)
Задача 1.18. Определить минимальную силу тяжести груза G, который при заливке формы чугуном нужно положить на верхнюю опоку, чтобы предотвратить ее всплывание. Вес верхней опоки Gon = 650 H. Плотность жидкого чугуна р = 7000 кг/м3. Вес чугуна в литниках и выпорах не учитывать. Размеры: a = 150 мм; b = 150 мм; D1 = 160 мм; D2 = 300 мм.
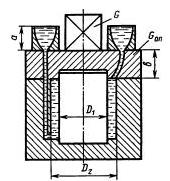
Ответ: G = 392 Н.
Скачать решение задачи 1.18 из Некрасова Б.Б (цена 60р)
Задача 1.19. Определить минимальную силу тяжести груза G, который при заливке формы чугуном нужно положить на верхний стержень, чтобы предотвратить его всплывание. Вес стержней с учетом веса чугуна в литнике и выпоре G1 = 50 Н. Плотность жидкого чугуна р = 7000 кг/м3; размеры: H = 200 мм; D=140 мм; h = 80 мм; d=120 мм.
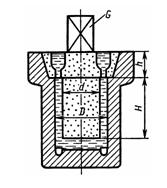
Ответ: G = 190 Н.
Скачать решение задачи 1.19 из Некрасова Б.Б (цена 60р)
Задача 1.20. В сосуде А и в трубе вода находится в покое; показание ртутного прибора hрт = 295 мм. Определить высоту H, если h=1 м.
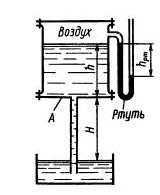
Ответ: Н = 3м.
Скачать решение задачи 1.20 из Некрасова Б.Б (цена 60р)
Задача 1.21. В герметичном сосуде-питателе А находится расплавленный баббит (р = 8000 кг/м3). При показании вакуумметра Pвак = 0,07 МПа заполнение различного ковша Б прекратилось. При этом H = 750 мм. Определить высоту уровня баббита h в сосуде-питателе A.
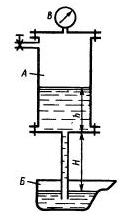
Ответ: h = 0,14 м.
Скачать решение задачи 1.21 из Некрасова Б.Б (цена 60р)
Задача 1.22. Избыточный напор газа на первом этаже дома составляет h1 = 100 мм вод. ст. Определить избыточный напор h2 газа на высоте H = 60 м, считая плотность воздуха и газа неизменными. Плотность газа рг = 0,70 кг/м3, воздуха рв=1,29 кг/м3.
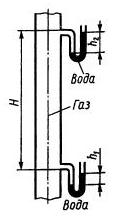
Ответ: hизб = 135 мм.вод.ст.
Скачать решение задачи 1.22 из Некрасова Б.Б (цена 60р)
Задача 1.23. Определить силу F, необходимую для удержания поршня на высоте h2 = 2 м над поверхностью воды в колодце. Над поршнем поднимается столб воды высотой h1 = 3 м. Диаметры: поршня D = 100 мм, штока d = 30 мм. Вес поршня и штока не учитывать.
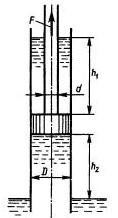
Ответ: F = 355 Н.
Скачать решение задачи 1.23 из Некрасова Б.Б (цена 60р)
Задача 1.24. В сосуде находится расплавленный свинец (р=11 г/см3). Определить силу давления, действующую на дно сосуда, если высота уровня свинца h = 500 мм, диаметр сосуда D = 400 мм, показание мановакуумметра Pвак = 30 кПа.
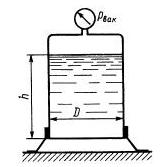
Ответ: F = 3,08 кН.
Скачать решение задачи 1.24 из Некрасова Б.Б (цена 60р)
Задача 1.25. Определить давление P1 жидкости, которую необходимо подвести к гидроцилиндру, чтобы преодолеть усилие, направленное вдоль штока F = 1 кН. Диаметры: цилиндра D = 50 мм, штока d = 25 мм. Давление в бачке P0 = 50 кПа, высота H0 = 5 м. Силу трения не учитывать. Плотность жидкости р=1000 кг/м3.
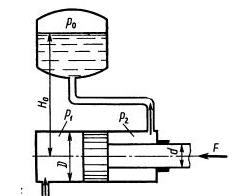
Ответ: Р1 = 0,584 МПа.
Скачать решение задачи 1.25 из Некрасова Б.Б (цена 60р)
Задача 1.26. Определить давление р в верхнем цилиндре гидропреобразователя (мультипликатора), если показание манометра, присоединенного к нижнему цилиндру, равно Pм = 0,48 МПа. Поршни перемещаются вверх, причем сила трения составляет 10 % от силы давления жидкости на нижний поршень. Вес поршней G = 4 кН. Диаметры поршней: D = 400 мм, d=100 мм; высота H = 2,5 м; плотность масла р = 900 кг/м3.
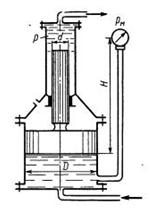
Ответ: Р2 = 6,57 МПа.
Скачать решение задачи 1.26 из Некрасова Б.Б (цена 60р)
Задача 1.27. Определить показание мановакуумметра рмв, если к штоку поршня приложена сила F = 0,1 кН, его диаметр d = 100 мм, высота H = 1,5 м, плотность жидкости р = 800 кг/м3.
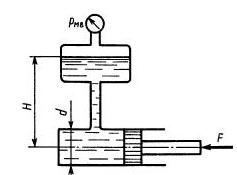
Ответ: Рвак = 0,96 кПа
Скачать решение задачи 1.27 из Некрасова Б.Б (цена 60р)
Задача 1.28. Определить силу, действующую на каждую из четырех стенок сосуда, имеющего форму перевернутой правильной пирамиды, если Pм = 0,5 МПа, H=4 м и h = 1,2 м; каждая сторона основания пирамиды b = 0,8 м. Плотность жидкости р = 800 кг/м3.
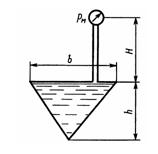
Ответ: F = 0,271 МН.
Скачать решение задачи 1.28 из Некрасова Б.Б (цена 60р)
Задача 1.29. Определить силы, действующие на верхние Fв и нижние Fн болты крышки, которая имеет форму прямоугольника высотой а = 0,64 м и шириной b = 1,5 м. Показание ртутного вакуумметра hрт=150 мм, высота h = 2,2 м.
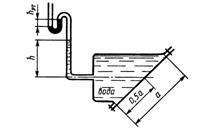
Ответ: Fв = 0,5 кН, Fн = 1 кН.
Скачать решение задачи 1.29 из Некрасова Б.Б (цена 60р)
Задача 1.30. Определить силу Р, действующую на шток гибкой диафрагмы, если ее диаметр D = 200 мм, показание вакуумметра рвак = 0,05 МПа, высота h=1 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если hа = 740 мм рт. ст.
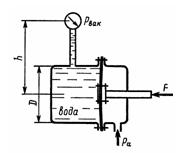
Ответ: F = -1,26 кН, Рабс = 58,4 кПа.
Скачать решение задачи 1.30 из Некрасова Б.Б (цена 60р)
Задача 1.31. Определить силу F на штоке золотника, если показание вакуумметра Pвак = 60 кПа, избыточное давление P1 = 1 МПа, высота H=3 м, диаметры поршней D = 20 мм и d = 15 мм, р = 1000 кг/м3.
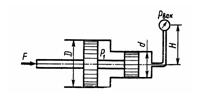
Ответ: F = 132 H.
Скачать решение задачи 1.31 из Некрасова Б.Б (цена 60р)
Задача 1.32. Система из двух поршней, соединенных штоком, находится в равновесии. Определить силу, сжимающую пружину. Жидкость, находящаяся между поршнями и в бачке - масло с плотностью р = 870 кг/м3. Диаметры: D = 80 мм; d = 30 мм; высота H=1000 мм; избыточное давление Pо=10 кПа.
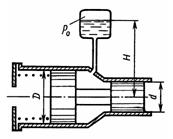
Ответ: F = 79,87 Н.
Скачать решение задачи 1.32 из Некрасова Б.Б (цена 60р)
Задача 1.33. Определить давление P1, необходимое для удержания штоком трехпозиционного гидроцилиндра нагрузки F = 50 кН; давление P2 = P3 = 0,3 кПа; диаметры: D = 40 мм, d = 20 мм.
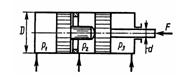
Ответ: Р1 = 40 МПа.
Скачать решение задачи 1.33 из Некрасова Б.Б (цена 60р)
Задача 1.34. Давление в цилиндре гидравлического пресса повышается в результате нагнетания в него жидкости ручным поршневым насосом и сжатия ее в цилиндре. Определить число двойных ходов n поршня ручного насоса, необходимое для увеличения силы прессования детали A от 0 до 0,8 МН, если диаметры поршней: D = 500 мм, d= 10 мм; ход поршня ручного насоса l = 30 мм; объемный модуль упругости жидкости K=1300 МПа; объем жидкости в прессе V=60 л. Чему равно максимальное усилие F на рукоятке насоса при ходе нагнетания, если b/а=10?
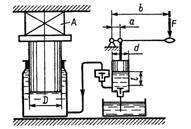
Ответ: n = 80, F = 31,4 Н.
Скачать решение задачи 1.34 из Некрасова Б.Б (цена 60р)
Задача 1.35. Определить нагрузку на болты крышек А и Б гидравлического цилиндра диаметром D= 160 мм, если к плунжеру диаметром d=120 мм приложена сила F = 20 кН.
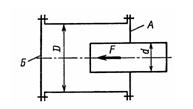
Ответ: FA = 15,3 кН, FБ = 35 кН.
Скачать решение задачи 1.35 из Некрасова Б.Б (цена 60р)
Задача 1.36. Определить давление рь необходимое для удержания цилиндром Ц нагрузки F = 70 кН. Противодавление в полости 2 равно P2 = 0,3 МПа, давление в полости 3 равно атмосферному. Размеры: Dц = 80 мм; Dш = 70 мм; d1 = 50 мм.
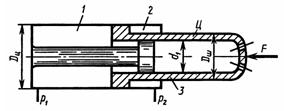
Ответ: Р1 = 22,9 МПа
Скачать решение задачи 1.36 из Некрасова Б.Б (цена 60р)
1 Гидростатика часть 2
Задача 1.37. На рисунке представлена конструктивная схема гидрозамка, проходное сечение которого открывается при подаче в полость A управляющего потока жидкости с давлением ру. Определить, при каком минимальном значении ру толкатель поршня 1 сможет открыть шариковый клапан, если известно: предварительное усилие пружины 2 F = 50 Н; D = 25 мм, d = 15 мм, P1 = 0,5 МПа, P2 = 0,2 МПа. Силами трения пренебречь.
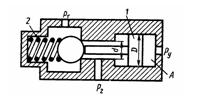
Ответ:Ру = 0,4 МПа.
Скачать решение задачи 1.37 из Некрасова Б.Б (цена 60р)
Задача 1.38. Определить, при какой высоте уровня воды начнет открываться клапан K, если сила пружины Fпр = 2 кН, угол ее установки α = 45°, высота h = 0,3 м. Труба перед клапаном имеет квадратное сечение со стороной а = 300 мм.
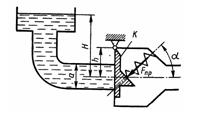
Ответ: Н = 1,58 м.
Скачать решение задачи 1.38 из Некрасова Б.Б (цена 60р)
Задача 1.39. Определить абсолютное давление в резервуаре 1, если подача жидкости из него по трубопроводу 2 прекратилась и клапан 3 закрылся. Показание вакуумметра Рвак = 0,05 МПа, высота H = 2,5 м, сила пружины Fпр=10 Н, плотность жидкости р = 800 кг/м3, атмосферное давление соответствует hа = 755 мм рт. ст., диаметры dкл = 20 мм, dш=10 мм. Вертикальными размерами клапана 3 пренебречь.
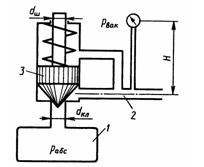
Ответ: Рабс = 109,77 кПа.
Скачать решение задачи 1.39 из Некрасова Б.Б (цена 60р)
Задача 1.40. Определить абсолютное давление на поверхности жидкости в сосуде и высоту h, если атмосферное давление соответствует hа = 740 мм рт. ст., поддерживающая сила F=10 Н, вес сосуда G = 2 Н, а его диаметр d = 60 мм. Толщиной стенки сосуда пренебречь. Плотность жидкости р=1000 кг/м3.
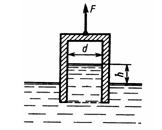
Ответ: Рабс = 96 кПа.
Скачать решение задачи 1.40 из Некрасова Б.Б (цена 60р)
Задача 1.41. Определить минимальное значение силы F, приложенной к штоку, под действием которой начнется движение поршня диаметром D = 80 мм, если сила пружины, прижимающая клапан к седлу, равна F0=100 Н, а давление жидкости P2 = 0,2 МПа. Диаметр входного отверстия клапана (седла) d1 = 10 мм. Диаметр штока d2 = 40 мм, давление жидкости в штоковой полости гидроцилиндра р1 = 1,0 МПа.
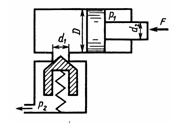
Ответ: Fmin = 3,64 кН.
Скачать решение задачи 1.41 из Некрасова Б.Б (цена 60р)
Задача 1.42. Определить величину предварительного поджатия пружины дифференциального предохранительного клапана (мм), обеспечивающую начало открытия клапана при Pн = 0,8 МПа. Диаметры клапана: D = 24 мм, d = 18 мм; жесткость пружины с = 6 Н/мм. Давление справа от большого и слева от малого поршней - атмосферное.
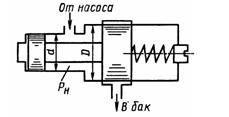
Ответ: х = 26,4мм.
Скачать решение задачи 1.42 из Некрасова Б.Б (цена 60р)
Задача 1.43. Для обеспечения обратного хода гидроцилиндра его полость 1 заполнена воздухом под начальным давлением P1. Найти размер l, определяющий положение стопорного кольца 2, которое ограничивает ход штока. Размеры цилиндра: Dц = 150 мм; dш = 130 мм; ход штока L = 400 мм. Сила трения поршня и штока 400 Н, давление слива P2 = 0,3 МПа, давление воздуха в начале обратного хода р1mах = 2 МПа. Процесс расширения и сжатия воздуха принять изотермическим.
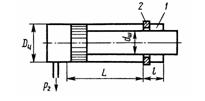
Ответ: l = 742 мм.
Скачать решение задачи 1.43 из Некрасова Б.Б (цена 60р)
Задача 1.44. Определить диаметр пяты dn плунжера аксиально-плунжерного насоса из условия безотрывного скольжения пяты по диску с 5 %-ным запасом по прижимающей силе. Закон распределения давления в зазоре принять линейным (см. эпюру). Диаметр плунжера d = 12 мм. Площадь отверстия в плунжере не учитывать.
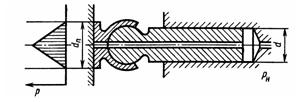
Ответ: dn = 20,3мм.
Скачать решение задачи 1.44 из Некрасова Б.Б (цена 60р)
Задача 1.45. Определить высоту h столба воды в пьезометрической трубке. Столб воды уравновешивает полый поршень D = 0,5 м и d = 0,2 м, имеющий высоту H = 0,3 м. Собственным весом поршня и трением в уплотнении пренебречь.
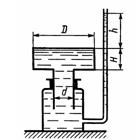
Ответ: h = 1,58м.
Скачать решение задачи 1.45 из Некрасова Б.Б (цена 60р)
Задача 1.46. Определить силу F, необходимую для удержания в равновесии поршня П, если труба под поршнем заполнена водой, а размеры трубы: D = 100 мм, H = 0,5 м; h = 4 м. Длины рычага: а = 0,2 м и b = 1,0 м. Собственным весом поршня пренебречь.
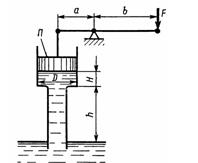
Ответ: F = 69,2 H.
Скачать решение задачи 1.46 из Некрасова Б.Б (цена 60р)
Задача 1.47. В системе дистанционного гидроуправления необходимо обеспечить ход l2 поршня В равным ходу l1 поршня A, т. е. l1 = l2 = l = 32 мм. Поршень В диаметром d = 20 мм должен действовать на рычаг С с силой F2 = 8 кН. Цилиндры и трубопровод заполнены маслом с модулем упругости K=1400 МПа. Объем масла, залитого при атмосферном давлении, V=700 см3. Определить диаметр D поршня А и силу F1, приложенную к поршню А. Упругостью стенок цилиндров и трубок, а также силами трения поршней о стенки цилиндров пренебречь.
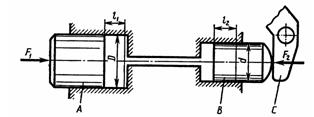
Ответ: D = 30мм, F1 = 1,8 кН.
Скачать решение задачи 1.47 из Некрасова Б.Б (цена 60р)
Задача 1.48. Определить объем гидроаккумулятора Vг =V1+V2, обеспечивающего выпуск штока гидроцилиндра против действия нагрузки F = 45 кН. Диаметры: цилиндра D = 120 мм; штока d = 60 мм; ход штока L = 1200 мм; давление на сливе Pс = 0,3 МПа. Процесс расширения воздуха считать изотермическим, максимальное давление в системе Pmах = 12 МПа.
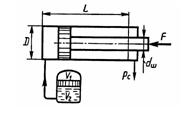
Ответ: V = 20,8 л.
Скачать решение задачи 1.48 из Некрасова Б.Б (цена 60р)
Задача 1.49. На рисунке представлена схема главного тормозного цилиндра автомобиля в момент торможения. Определить силу А, которую необходимо приложить к педали тормоза, чтобы давление в рабочих цилиндрах передних колес было P1 = 6 МПа. Каким при этом будет давление в рабочих цилиндрах задних колес P2? При расчете принять: усилие пружины F1=100 Н, пружины 2 F2=150 Н, d = 20 мм, а = 60 мм, b=180 мм. Силами трения пренебречь.
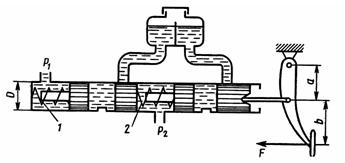
Ответ: F =493 H, P2 = 5,8 МПа.
Скачать решение задачи 1.49 из Некрасова Б.Б (цена 60р)
Задача 1.50. На рисунке показана принципиальная схема гидровакуумного усилителя гидропривода тормозов автомобиля. Давление жидкости, создаваемое в гидроцилиндре 1 благодаря нажатию на ножную педаль с силой Р, передается в левую полость тормозного гидроцилиндра 2. Помимо давления жидкости на поршень 3 в том же направлении действует сила вдоль штока 4, связанного с диафрагмой 5. Последняя отделяет полость A, сообщающуюся с атмосферой, от полости Б, где устанавливается вакуум благодаря соединению ее со всасывающим коллектором двигателя при нажатии на педаль. Пружина 6 при этом действует на диафрагму справа налево с силой Fпр. Определить давление жидкости, подаваемой из правой полости гидроцилиндра 2 к колесным тормозным цилиндрам. Принять: усилие педали F = 200 Н; сила пружины 6 Fпр = 20 Н; давление в полости Б Pвак = 0,06 МПа; диаметры: диафрагмы D = 100 мм, гидроцилиндра 1 d1=25 мм и гидроцилиндра 2 d2 = 20 мм; отношение плеч Площадью сечения штока 4 пренебречь.
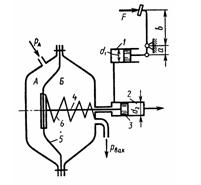
Ответ: Р = 3,48 МПа.
Скачать решение задачи 1.50 из Некрасова Б.Б (цена 60р)
Задача 1.51. Определить диаметр D резервуаров-накопителей 1 пневматической системы тормозов автомобиля (трактора), при котором будет обеспечиваться шесть торможений за счет сжатого воздуха без включения компрессора 2. Последний включается и начинает нагнетать воздух в систему при избыточном давлении p1 = 0,4 МПа и выключается при Р2 = 0,6 МПа. Кран управления 3 после каждого торможения выпускает воздух из тормозных цилиндров 4 в атмосферу. Принять: диаметр тормозных камер d=180 мм, ходы поршней l = 0,06 м, длины резервуаров L = 0,8 мм, атмосферное давление соответствует ha = 749,5 мм рт. ст. Процесс расширения воздуха считать изотермическим. Объемом трубопроводов пренебречь. Определить, сколько полных торможений без включения компрессора могут обеспечить эти резервуары, если автомобиль въехал на горный перевал (где hа = 400 мм рт. ст.) без использования тормозной системы.
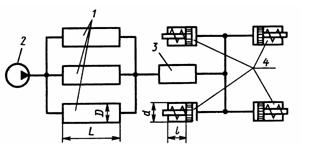
Ответ: D = 200 мм, n = 8.
Скачать решение задачи 1.51 из Некрасова Б.Б (цена 60р)
Задача 1.52. Топливный бак автомобиля длиной L = 0,6 м, шириной 6 = 0,5 м и высотой H = 0,2 м движется с ускорением а = 3,27 м/с2. Определить минимальное количество топлива в баке, обеспечивающее его подачу без подсоса воздуха. Считать, что бензопровод установлен в центре горизонтальной проекции бака, его диаметр мал по сравнению с длиной бака, h = 10 мм.
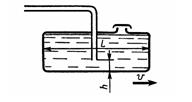
Ответ: V = 9,1 л.
Скачать решение задачи 1.52 из Некрасова Б.Б (цена 60р)
Задача 1.53. Определить расположение центра тяжести С бетонного раствора (hc и lс), залитого в закрытый кузов автомобиля при его торможении с ускорением а = g. Считать, что кузов имеет форму параллелепипеда: L = 1,92 м, H = 1,2 м и h = 1 м.
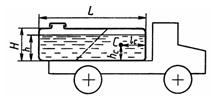
Ответ: Lc = 0,84м, hc = 0,6м
Скачать решение задачи 1.53 из Некрасова Б.Б (цена 60р)
Задача 1.54. Цилиндрический сосуд, заполненный жидкостью с плотностью р=900 кг/м3, движется с ускорением а = 4g. Определить силы, действующие на крышки А и Б, если L= 1 м и D = 0,5 м. Избыточное давление в точке 1 считать равным нулю.
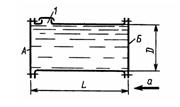
Ответ: FA = 0,43 кН, FБ = 7,49 кН.
Скачать решение задачи 1.54 из Некрасова Б.Б (цена 60р)
Задача 1.55. В кузов автомобиля-самосвала до уровня h1 = 0,4 м налит цементный раствор. Определить наименьший допустимый путь торможения самосвала от скорости v = 36 км/ч до остановки исходя из условия, что раствор не выплеснулся из кузова. Для упрощения принять, что кузов самосвала имеет форму прямоугольной коробки размерами l = 2,5 м; h = 0,8 м; ширина кузова b = 1,8 м, а движение автомобиля при торможении равнозамедленное.
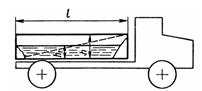
Ответ: Smin = 15,9м.
Скачать решение задачи 1.55 из Некрасова Б.Б (цена 60р)
Задача 1.56. На рисунке показан элемент одной из возможных схем гидроусилителя сцепления автомобиля (трактора). Масло под давлением р0 = 0,5 МПа подводится внутрь вала и затем через отверстие - в полость между двумя совместно вращающимися цилиндром А и поршнем Б, который может скользить вдоль вала. Давление масла, увеличенное благодаря действию центробежных сил, заставляет поршень перемещаться вправо и обеспечивает этим силу нажатия, необходимую для включения сцепления. Определить силу давления масла на поршень Б, если его диаметр D = 120 мм, диаметр вала d = 20 мм, частота вращения n = 6000 об/мин, плотность рм = 920 кг/м3.
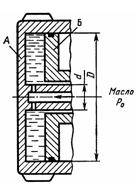
Ответ: F = 9,27 кН
Скачать решение задачи 1.56 из Некрасова Б.Б (цена 60р)
Задача 1.57. В машину для центробежной отливки подшипниковых втулок залита расплавленная бронза (р = 8000 кг/м3). Определить силу, воспринимаемую болтами A, если шпиндель вращается с частотой n=1000 об/мин, диаметры: D = 150 мм, d =100 мм.
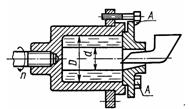
Ответ: F = 660 H.
Скачать решение задачи 1.57 из Некрасова Б.Б (цена 60р)
Задача 1.58. В сосуд высотой H = 0,3 м залита жидкость до уровня h = 0,2 м. Определить, до какой угловой скорости со можно раскрутить сосуд, с тем чтобы жидкость не выплеснулась из него, если его диаметр D =100 мм.
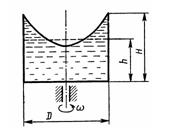
Ответ: w = 39,6 с-1.
Скачать решение задачи 1.58 из Некрасова Б.Б (цена 60р)
Задача 1.59. При отливке цилиндрической полой заготовки во вращающейся относительно вертикальной оси форме из-за действия сил тяжести нижний внутренний радиус r1 будет меньше верхнего внутреннего радиуса r2. Определить их разность, если высота отливки H = 0,5 м, форма вращается с угловой скоростью (w = 200 с-1), ее диаметр D = 200 мм и она в начальный момент заполнена на 30 % своего объема.
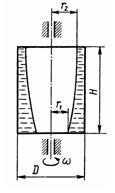
Ответ: Δr = 1,5 мм.
Скачать решение задачи 1.59 из Некрасова Б.Б (цена 60р)
Задача 1.60. Цилиндрический сосуд диаметром D = 80 мм вращается на вертикальном валу диаметром d = 30 мм. Определить минимальную угловую скорость w, при которой жидкость не будет соприкасаться с валом, если первоначально сосуд был заполнен до уровня h = 0,05 м. Считать, что высота сосуда H достаточно велика, чтобы при этой угловой скорости жидкость не доставала до крышки сосуда.
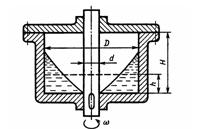
Ответ: w = 32,8 с-1.
Скачать решение задачи 1.60 из Некрасова Б.Б (цена 60р)
Задача 1.61. Определить минимальную частоту вращения n, которую нужно сообщить сосуду, изображенному на схеме, вокруг его вертикальной оси для полного его опорожнения. Размеры: D = 200 мм; d = 100 мм; H = 50 мм.
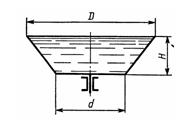
Ответ: nmin = 133,75 об/мин.
Скачать решение задачи 1.61 из Некрасова Б.Б (цена 60р)
Задача 1.62. Определить минимальную угловую скорость литейной формы w, при которой шлак и легкие включения (плотностью р2) будут иметь возможность выделиться из расплавленного металла (плотностью р1) в середину формы. Размеры отливаемой детали: D1=300 мм; D2 = 200 мм; H = 300 мм.
Указание. Легкие включения могут перемещаться к центру формы лишь в том случае, если равнодействующая архимедовой и центростремительной сил будет иметь составляющую, направленную вдоль стенки вниз, т. е. если α≥90°.
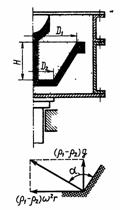
Ответ: nmin = 232 об/мин.
Скачать решение задачи 1.62 из Некрасова Б.Б (цена 60р)
Задача 1.63. Ротор центрифуги, включенной в систему смазки двигателя внутреннего сгорания для очистки масла, представляет собой полый цилиндр, заполненный маслом и вращающийся с частотой n = 7000 об/мин (рм = 900 кг/м3). Определить давление р масла на внутренней боковой поверхности ротора и силу давления Р, действующую на крышку ротора, если диаметры D=140 мм, d = 30 мм. Масло подводится к центрифуге под давлением P0= 05 МПа.
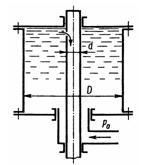
Ответ: Р = 1,63 МПа, F = 12 кН.
Скачать решение задачи 1.63 из Некрасова Б.Б (цена 60р)
2 Применение уравнения Бернулли
Задача 2.1. Из напорного бака вода течет по трубе диаметром d1 = 20 мм и затем вытекает в атмосферу через насадок (брандспойт) с диаметром выходного отверстия d2 = 10 мм. Избыточное давление воздуха в баке P0 = 0,18 МПа; высота H = 1,6 м. Пренебрегая потерями энергии, определить скорости течения воды в трубе v1 и на выходе из насадка v2.
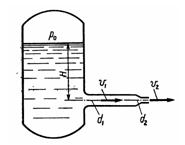
Ответ: v2 = 19,8 м/с, v1 = 4,96 м/с.
Скачать решение задачи 2.1 из Некрасова Б.Б (цена 70р)
Задача 2.2. Определить расход керосина, вытекающего из бака по трубопроводу диаметром d = 50 мм, если избыточное давление воздуха в баке P0 = 16 кПа; высота уровня Hо= 1 м; высота подъема керосина в пьезометре, открытом в атмосферу, H=1,75 м. Потерями энергии пренебречь. Плотность керосина р = 800 кг/м3.
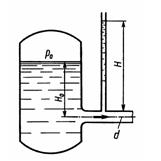
Ответ: v = 5 м/с, Q = 9,8 л/с.
Скачать решение задачи 2.2 из Некрасова Б.Б (цена 70р)
Задача 2.3. К расходомеру Вентури присоединены два пьезометра и дифференциальный ртутный манометр. Выразить расход воды Q через размеры расходомера D и d, разность показаний пьезометров H, а также через показание дифференциального манометра h. Дан коэффициент сопротивления участка между сечениями 1-1 и 2-2.
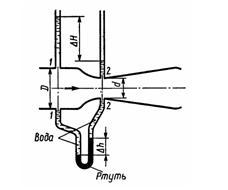
Скачать решение задачи 2.3 из Некрасова Б.Б (цена 70р)
Задача 2.4. Определить весовой расход воздуха по трубе с плавно закругленным входом и цилиндрической частью диаметром D = 200 мм, если показание вакуумметра в виде вертикальной стеклянной трубки, опущенной в сосуд с водой, h = 250 мм. Коэффициент сопротивления входной части трубы (до места присоединения вакуумметра) ξ = 0,1. Плотность воздуха рвоз = 1,25 кг/м3.
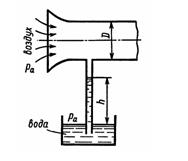
Ответ: v = 59,5 м/с, G = 2,34 кг/с.
Скачать решение задачи 2.4 из Некрасова Б.Б (цена 70р)
Задача 2.5. От бака, в котором с помощью насоса поддерживается постоянное давление жидкости, отходит трубопровод диаметром d = 50 мм. Между баком и краном К на трубопроводе установлен манометр. При закрытом положении крана P0 = 0,5 МПа. Найти связь между расходом жидкости в трубопроводе Q и показанием манометра р при разных открытиях крана, приняв коэффициент сопротивления входного участка трубопровода (от бака до манометра) равным 0,5. Плотность жидкости р = 800 кг/м3. Подсчитать расход жидкости при полном открытии крана, когда показание манометра равно р = 0,485 МПа.
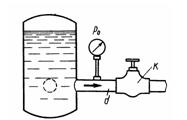
Ответ: v = 5м/с, Q = 9,8 л/с.
Скачать решение задачи 2.5 из Некрасова Б.Б (цена 70р)
Задача 2.6. Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте H = 2 м и постоянное давление P2 = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d1 = 75 мм, показывает P1 = 0,25 МПа. Определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку, равен d2 = 50 мм; коэффициент сопротивления этой трубы принят равным 0,5. Плотность жидкости р = 800 кг/м3.
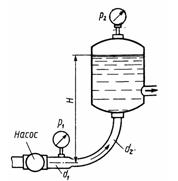
Ответ: Q = 33 л/с.
Скачать решение задачи 2.6 из Некрасова Б.Б (цена 70р)
Задача 2.7. Жидкость вытекает из открытого резервуара в атмосферу через трубу, имеющую плавное сужение до диаметра d1, а затем постепенное расширение до d2. Истечение происходит под действием напора H = 3 м. Пренебрегая потерями энергии, определить абсолютное давление в узком сечении трубы 1-1, если соотношение диаметров d2/d1=20,5; атмосферное давление соответствует Pа = 750 мм рт. ст.; плотность жидкости р=1000 кг/м3. Найти напор Hкр, при котором абсолютное давление в сечении 1-1 будет равно нулю.
Указание. Уравнение Бернулли следует записать два раза, например для сечения 0 - 0 и 2 - 2, а затем для сечений 1-1 и 2 - 2.
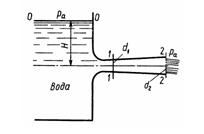
Ответ: Р = 0,012 МПа, Нкр = 1,74м.
Скачать решение задачи 2.7 из Некрасова Б.Б (цена 70р)
Задача 2.8. Вода перетекает из напорного бака, где избыточное давление воздуха р = 0,3 МПа, в открытый резервуар по короткой трубе диаметром d = 50 мм, на которой установлен кран. Чему должен быть равен коэффициент сопротивления крана для того, чтобы расход воды составлял Q = 8,7 л/с? Высоты уровней Н1 = 1 м и H2 = 3 м. Учесть потерю напора на входе в трубу (ξвх = 0,5) и на выходе из трубы (внезапное расширение).
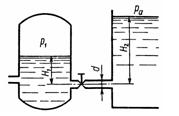
Ответ: ξкр = 27,5.
Скачать решение задачи 2.8 из Некрасова Б.Б (цена 70р)
Задача 2.9. Жидкость должна перетекать из резервуара A, где поддерживается постоянный уровень Н1, в емкость Б. Для этой цели в дне резервуара устроено отверстие с закругленными входными кромками (ξ0 = 0,05). Но расход жидкости через это отверстие оказался недостаточным. Каким способом и во сколько раз можно увеличить расход через отверстие, не меняя его диаметра и напора? Высота расположения выходного отверстия относительно нижнего уровня Н2 = Н1.
Указание. Следует установить диффузор (как показано пунктиром), который даст возможность использовать дополнительный напор H2 и превратить большую часть скоростного напора в давление (создать разрежение в горловине диффузора и, следовательно, эффект подсоса).
Принять коэффициент сопротивления диффузора равным ξдиф = 0,2 (отнесено к скорости в узком сечении), а степень расширения диффузора достаточно большой, чтобы можно было пренебречь скоростным напором на выходе из диффузора.
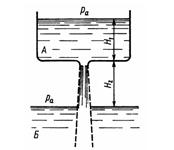
Ответ: Q2/Q1 = 2,9.
Скачать решение задачи 2.9 из Некрасова Б.Б (цена 70р)
Задача 2.10. Для измерения расхода воды, которая подается по трубе А в бак Б, установлен расходомер Вентури В. Определить максимальный расход, который можно пропускать через данный расходомер при условии отсутствия в нем кавитации, если температура воды t = 60°С (давление насыщенных паров соответствует hнп = 2 м вод. ст.). Уровень воды в баке поддерживается постоянным, равным H = 1,5 м; h = 0,5 м. Размеры расходомера: d1 = 50 мм; d2 = 20 мм. Атмосферное давление принять равным 760 мм рт. ст. Коэффициент сопротивления диффузора
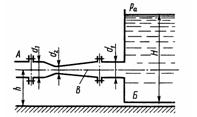
Ответ: Qmax = 4,8 л/с.
Скачать решение задачи 2.10 из Некрасова Б.Б (цена 70р)
Задача 2.11. Вода (р = 1000 кг/м3) перетекает из верхнего резервуара в нижний по расширяющейся трубе - диффузору, имеющему малый угол конусности и плавно закругленный вход. Пренебрегая потерей напора на входе в диффузор, определить, при каком уровне воды Н1 в верхнем резервуаре абсолютное давление в узком сечении 1-1 диффузора сделается равным нулю. Коэффициент сопротивления диффузора ξдиф = 0,2. Размеры: d1 = 100 мм; d2 = 150 мм; H2 = 1,15 м. Учесть потерю на внезапное расширение при выходе из диффузора. Атмосферное давление 750 мм рт. ст.
Указание. Учесть потерю кинетической энергии на выходе из диффузора по формуле Борда.
Ответ: Н1 = 4,6м.
Скачать решение задачи 2.11 из Некрасова Б.Б (цена 70р)
Задача 2.12. Бензин сливается из цистерны по трубе диаметром d = 50 мм, на которой установлен кран с коэффициентом сопротивления ξкр = 3. Определить расход бензина при H1 = 1,5 м и H2 = 1,3 м, если в верхней части цистерны имеет место вакуум hвак = 73,5 мм рт. ст. Потерями на трение в трубе пренебречь. Плотность бензина р = 750 кг/м3.
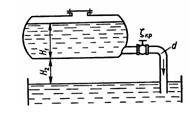
Ответ: v = 2,53 м/с, Q = 4,97 л/с.
Скачать решение задачи 2.12 из Некрасова Б.Б (цена 70р)
Задача 2.13. Определить расход воды, вытекающей из бака через короткую трубку (насадок) диаметром d = 30 мм и коэффициентом сопротивления ξ = 0,5, если показание ртутного манометра hрт=1,47 м; Н1 = 1 м; H0 =1,9 м; L = 0,1 м.
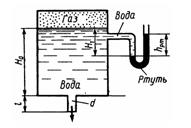
Ответ: v = 16,6 м/с, Q = 11,7 л/с.
Скачать решение задачи 2.13 из Некрасова Б.Б (цена 70р)
Задача 2.14. При внезапном расширении трубы от d до D получается увеличение давления, которому соответствует разность показаний пьезометров H. Определить, при каком соотношении площадей широкого и узкого сечений трубы (n = D2/d2) увеличение давления будет наибольшим. Выразить величину Hmах через скорость в узком сечении.
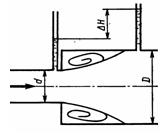
Ответ: n = 2.
Скачать решение задачи 2.14 из Некрасова Б.Б (цена 70р)
Задача 2.15. Сравнить коэффициенты сопротивления мерного сопла d, установленного в трубе D, и расходомера Вентури, состоящего из такого же сопла диаметром d, и диффузора. Коэффициенты сопротивления определить как отношение суммарной потери напора к скоростному напору в трубопроводе. Дано отношение диаметров D/d = 2. Принять коэффициенты сопротивлений: сопла ξс = 0,05; диффузора ξдиф = 0,15 (оба коэффициента относятся к скорости в узком сечении). Определить потери напора, вызываемые мерным соплом hс и расходомером hР, при одинаковой скорости потока в трубе v = 3 м/с.
Указание. На выходе из сопла учесть потери напора на внезапное расширение.
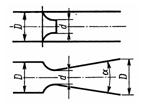
Ответ: ξс = 9,8, ξр = 2,4.
Скачать решение задачи 2.15 из Некрасова Б.Б (цена 70р)
Задача 2.16. Сравнить коэффициенты сопротивления расходомера Вентури, данные которого приведены в предыдущей задаче, и специального расходомера, показанного на рисунке. Последний состоит из диффузора (ξдиф = 0,15), расширяющего поток до диаметра d1 = 1,4d, внезапного расширения широкой части до диаметра D = 2,5d, в которой установлена решетка для выравнивания скоростей (ξр = 0,05) и сопла (ξс = 0,05). Коэффициенты отнесены к скорости в трубе диаметров d.
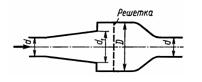
Ответ: ξ = 0,275.
Скачать решение задачи 2.16 из Некрасова Б.Б (цена 70р)
Задача 2.17. Определить расход жидкости, вытекающей из трубы диаметром d=16 мм через плавное расширение (диффузор) и далее по трубе диаметром D = 20 мм в бак. Коэффициент сопротивления диффузора 0,2 (отнесен к скорости в трубе), показание манометра рм = 20 кПа; высота h = 0,5 м; H = 5 м; плотность жидкости р=1000 кг/м3. Учесть потери на внезапное расширение, потерями на трение пренебречь, режим течения считать турбулентным.
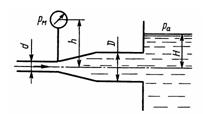
Ответ: Q = 2,1 л/с.
Скачать решение задачи 2.17 из Некрасова Б.Б (цена 70р)
Задача 2.18. Вода перетекает из бака А в резервуар Б по трубе длиной l = 2,5 м и диаметром d = 25 мм, на которой установлены вентиль (ξв = 3,5) и диффузор с углом α = 8° и диаметром выходного отверстия D = 75 мм. Показание мановакуумметра рвак = 10 кПа; высота H = 2,5 м, h = 2 м. Определить расход Q с учетом всех местных сопротивлений и трения по длине (λ = 0,03). Вход в трубу без закруглений, радиус кривизны колен R = 25 мм. Взаимным влиянием сопротивлений пренебречь.
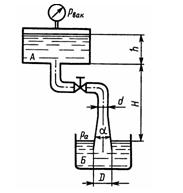
Ответ: Q = 1,29 л/с.
Скачать решение задачи 2.18 из Некрасова Б.Б (цена 70р)
Задача 2.19. Вода перетекает из напорного бака А в резервуар Б через вентиль с коэффициентом сопротивления ξв = 3 по трубе. Диаметры: d1 = 40 мм; d2 = 60 мм. Считая режим течения турбулентным и пренебрегая потерями на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Высоты: Н1 = 1 м, H2 = 2 м; избыточное давление в напорном баке P0 = 0,15 МПа.
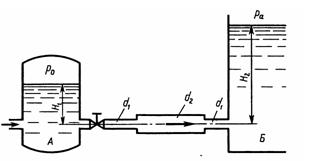
Ответ: Q = 9,3 л/с.
Скачать решение задачи 2.19 из Некрасова Б.Б (цена 70р)
Задача 2.20. Пренебрегая потерями напора, определить степень расширения диффузора n = (D/d)2, при котором давление в сечении 2-2 возрастет в два раза по сравнению с давлением в сечении 1-1. Расчет провести при следующих данных: расход жидкости Q = 1,5 л/с; диаметр d = 20 мм; давление в сечении 1-1 P1 = 10 кПа; плотность жидкости р = 1000 кг/м3; режим течения принять: а) ламинарным и б) турбулентным. Поток в диффузоре считать стабилизированным и безотрывным.
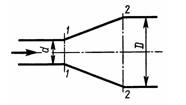
Ответ: nл = 1,33, nт = 2,84.
Скачать решение задачи 2.20 из Некрасова Б.Б (цена 70р)
Задача 2.21. Определить минимальное давление рм, измеряемое манометром перед сужением трубы, при котором будет происходить подсасывание воды из резервуара А в узком сечении трубы. Размеры: d1 = 60 мм; d2 = 20 мм; Н1 = 6 м; H2 = 1 м. Принять коэффициенты сопротивления: сопла ξс = 0,08, диффузора ξдиф = 0,30.
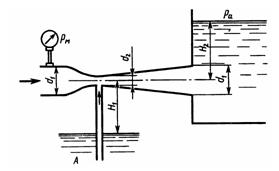
Ответ: Рм = 51,5 кПа.
Скачать решение задачи 2.21 из Некрасова Б.Б (цена 70р)
Задача 2.22. По длинной трубе диаметром d = 50 мм протекает жидкость (v = 2 Ст; р = 900 кг/м3). Определить расход жидкости и давление в сечении, где установлены пьезометр (h = 60 см) и трубка Пито (H = 80 см).
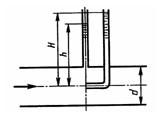
Ответ: Q = 2,75 л/с, Р = 5,3 кПа.
Скачать решение задачи 2.22 из Некрасова Б.Б (цена 70р)
Задача 2.23. Определить потерю давления в диффузоре с начальным d=10 мм и конечным D= 20 мм диаметрами, если вязкость жидкости v=1 Ст; плотность р = 900 кг/м3; расход Q=1 л/с; угол диффузора α = 5°. При решении задачи считать, что в любом сечении диффузора существует стабилизированное ламинарное течение и справедлив закон Пуазейля.
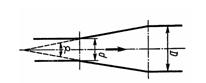
Ответ: ΔРтр = 11 кПа.
Скачать решение задачи 2.23 из Некрасова Б.Б (цена 70р)
Задача 2.24. Вода течет по трубе диаметром D = 20 мм, имеющей отвод (d = 8 мм). Пренебрегая потерями напора, определить расход жидкости в отводе Q/, если расход в основной трубе Q=1,2 л/с; высоты H = 2 м, h = 0,5 м. Режим течения считать турбулентным.
Указание. Считать, что давление перед отводом расходуется на создание скоростного напора в отводе и подъем жидкости на высоту Н.
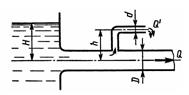
Ответ: Q/ = 194 см3/с.
Скачать решение задачи 2.24 из Некрасова Б.Б (цена 70р)
Задача 2.25. Жидкость вытекает из трубы с диаметром d, на конце которой укреплена круглая шайба 1 с диаметром D. На расстоянии h=1/4 от этой шайбы помещен диск 2 того же диаметра D. Поток наталкивается на этот диск, после чего жидкость растекается радиально между двумя плоскостями и затем выходит в атмосферу. Расход и плотность жидкости заданы. Найти закон изменения давления вдоль радиуса диска, считая жидкость идеальной. Принять течение радиальным и безотрывным. Выразить силу, с которой диск притягивается к шайбе, с учетом удара жидкости о диск при изменении осевого движения на радиальное.
Указание. Для нахождения силы применить уравнение количества движения.
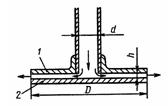
Скачать решение задачи 2.25 из Некрасова Б.Б (цена 70р)
Задача 2.26. На рисунке показана схема водоструйного насоса-эжектора. Вода под давлением р0 подводится по трубе диаметром d = 40 мм в количестве Q. Сопло сужает поток до dс=15 мм и тем самым увеличивает скорость, понижая давление. Затем в диффузоре происходит расширение потока до d = 40 мм и повышение давления. Вода выходит в атмосферу на высоте H2 = 1 м. Таким образом в камере K создается вакуум, который заставляет воду подниматься из нижнего резервуара на высоту H1=3 м. Определить минимальное давление P0 перед эжектором, при котором возможен подъем воды на высоту Н1. Учесть потери напора в сопле (ξс = 0,06), в диффузоре (ξдиф = 0,25) и в коленах (ξк = 0,25) для каждого. Коэффициенты отнесены к скорости в трубе с диаметром d.
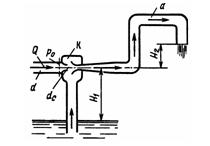
Ответ: Р0min = 0,01 МПа.
Скачать решение задачи 2.26 из Некрасова Б.Б (цена 70р)
Задача 2.27. Жидкость с плотностью р=1000 кг/м3 протекает по металлической трубе с диаметром dт= 10 мм, а затем по резиновому шлангу, который имеет начальный диаметр dш= 10 мм. Под действием давления жидкости рч резиновый шланг растягивается до диаметра D. Жесткость шланга на диаметральное растяжение с = P2*π*D*l/б = 3*106 Н/м, где б - приращение диаметра шланга l = 1 м. Определить диаметр шланга О, если давление р1 = 0,1 МПа; расход жидкости Q=1,2 л/с.
Указание. Задачу решить методом последовательных приближений, задаваясь величиной D. Потерями пренебречь.
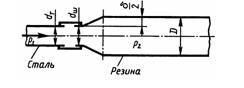
Ответ: D = 12мм
Скачать решение задачи 2.27 из Некрасова Б.Б (цена 70р)
Задача 2.28. Для определения потерь давления на фильтре установлены манометры, как показано на рисунке. При пропускании через фильтр жидкости, расход которой Q = 1 л/с; давления: P1 = 0,1 МПа, P2 = 0,12 МПа. Определить, чему равна потеря давления в фильтре, если известно: d1 = 10 мм, d2 = 20 мм, рж = 900 кг/м3.
Указание. Потерей давления на участках от мест установки манометров до фильтра пренебречь. Принять α1 = α2 = 1.
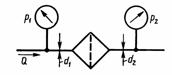
Ответ: ΔРф = 0,05 МПа.
Скачать решение задачи 2.28 из Некрасова Б.Б (цена 70р)
Задача 2.29. В гидросистеме с расходом масла Q = 0,628 л/с параллельно фильтру 1 установлен переливной клапан 2, открывающийся при перепаде давления на P = 0,2 МПа. Определить вязкость v, при которой начнется открытие клапана, если коэффициент сопротивления фильтра связан с числом Рейнольдса формулой λф = А/Rе, где А = 2640; Rе подсчитывается по диаметру трубы d = 20 мм; р = 850 кг/м3.
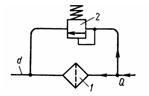
Ответ: v = 17,8 Ст.
Скачать решение задачи 2.29 из Некрасова Б.Б (цена 70р)
Задача 2.30. Определить коэффициент сопротивления жиклера с конической входной частью (d1=2 мм; l = 6 мм), установленного в трубе (d2=10 мм), если число Рейнольдса потока жидкости в трубе Rе=100. Искомый коэффициент рассматривать как отношение потери напора в жиклере к скоростному напору в трубке диаметром d2.
Указание. Потерю напора в жиклере выразить как сумму двух потерь: на трение по длине l и на внезапное расширение до нулевой скорости. Поток в жиклере считать стабилизированным.
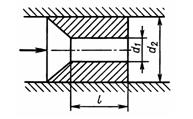
Ответ ξж = 1490.
Скачать решение задачи 2.30 из Некрасова Б.Б (цена 70р)
Задача 2.31. Определить максимально возможную секундную утечку жидкости через зазор между насосным плунжером и цилиндром, если диаметр плунжера d = 20 мм; радиальный зазор при соосном расположении плунжера и цилиндра а = 0,01 мм; свойства жидкости: v = 0,01 Ст; р = 800 кг/м3. Давление, создаваемое насосом, р = 25 МПа; длина зазора L = 30 мм. Указание. Использовать формулу (2.13), а также комментарий к ней.
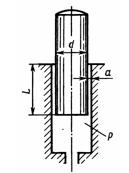
Ответ: С учет максимального эксцентриситета Q = 13,6 см3/с.
Скачать решение задачи 2.31 из Некрасова Б.Б (цена 70р)
Задача 2.32. Определить напор, создаваемый насосом системы охлаждения автомобильного двигателя, при следующих данных: подача насоса Q = 3,9 л/с; коэффициенты сопротивления: блока цилиндров ξ1=3,5; термостата ξ2 = 2,5; радиатора ξ3 = 4,0; трубы (шланга) от радиатора до насоса ξ4 = 2,0. Все коэффициенты отнесены к скорости в трубе диаметром d = 40 мм. Чему равно абсолютное давление перед входом в насос, если в верхней части радиатора возник вакуум рвак=1 кПа; высота H = 0,4 м; атмосферное давление соответствует hа = 750 мм рт. ст., рж=1000 кг/м3?
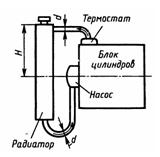
Ответ: Нн = 6,1м, Рабс = 0,07 МПа.
Скачать решение задачи 2.32 из Некрасова Б.Б (цена 70р)
Задача 2.33. Воздух засасывается двигателем из атмосферы, проходит через воздухоочиститель и затем по трубе диаметром d1 = 50 мм подается к карбюратору. Плотность воздуха р = 1,28 кг/м3. Определить разрежение в горловине диффузора диаметром d2 = 25 мм (сечение 2-2) при расходе воздуха Q = 0,05м3/с. Принять следующие коэффициенты сопротивления: воздухоочистителя ξ1 = 5; колена ξ2 = 1; воздушной заслонки ξ3 = 0,5 (отнесены к скорости в трубе); сопла ξ4 = 0,05 (отнесен к скорости в горловине диффузора).
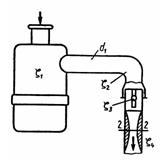
Ответ: Рвак = 9,7 кПа.
Скачать решение задачи 2.33 из Некрасова Б.Б (цена 70р)
Задача 2.34. На рисунке показана схема двойного диффузора карбюратора, который обеспечивает больший вакуум, чем одинарный. Выходное сечение малого и узкое сечение большого диффузоров совпадают; в узком сечении малого диффузора расположен обрез распылителя бензина (наклонная трубка). Определить величину разрежения в сечении 1-1 при расходе воздуха G = 2 Н/с и следующих размерах: D = 40 мм; d1 = 12 мм; d2 = 20 мм. Принять следующие значения коэффициентов сопротивления участков воздушного потока: от 0-0 при Pо=Pа и 0 = 0 до 1-1 ξ1 = 0,1; от 1-1 до 2-2 (внутри малого диффузора) ξ2 = 0,2 (отнесены к площади π*d12/4); от 0-0 до 2-2 (горловины большого диффузора) ξ3 = 0,12 (отнесено к площади π*(D2-d22)/4). Воздух считать несжимаемым, плотность рвоз=1,25 кг/м3. Давление в горловине большого диффузора (2-2) считать равным давлению на выходе из малого диффузора.
Указание. Следует записать уравнение суммы расходов через диффузоры G1 и G2 и уравнения Бернулли для воздушных потоков от 0-0 до 2-2 внутри малого диффузора и вне его. Система трех уравнений с тремя неизвестными G1, G2 и pa - р2 позволяет найти расход через малый диффузор G1. Затем из уравнения Бернулли для сечений 1-1 и 2-2 (внутри малого диффузора) определяется искомое разрежение (вакуум) ра – р1. Расходом бензина пренебречь.
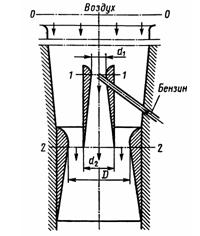
Ответ: Рвак = 20 кПа.
Скачать решение задачи 2.34 из Некрасова Б.Б (цена 90р)
3 Истечение жидкости через отверстия, насадки, дроссели и клапаны часть 1
Задача 3.1. Определить расход жидкости (р = 800 кг/м3), вытекающей из бака через отверстие площадью S0=1 см2. Показание ртутного прибора, измеряющего давление воздуха, h = 268 мм, высота Н = 2 м, коэффициент расхода отверстия μ = 0,60.
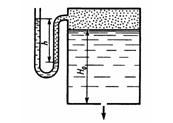
Ответ: Q = 0,68 л/с.
Скачать решение задачи 3.1 из Некрасова Б.Б (цена 70р)
Задача 3.2. Определить скорость перемещения поршня вниз, если к его штоку приложена сила F = 10 кН. Поршень диаметром D = 50 мм имеет пять отверстий диаметром d0 = 2 мм каждое. Отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода μ = 0,82; р = 900 кг/м3.
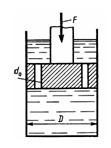
Ответ: v = 0,528 м/с.
Скачать решение задачи 3.2 из Некрасова Б.Б (цена 70р)
Задача 3.3. Определить направление истечения жидкости (р = рвод) через отверстие d0=5 мм и расход, если разность уровней H = 2 м, показание вакуумметра Pвак соответствует 147 мм рт. ст., показание манометра Pм = 0,25 МПа, коэффициент расхода μ = 0,62.
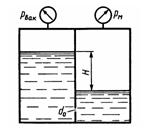
Ответ: Q = 0,27 л/с.
Скачать решение задачи 3.3 из Некрасова Б.Б (цена 70р)
Задача 3.4. Определить коэффициент сопротивления многоступенчатого дросселя, отнесенный к скорости в трубке диаметром d= 10 мм, если дроссель состоит из пяти ступеней. Каждая ступень представляет собой отверстие диаметром d0 = 2 мм в стенке толщиной б = 1,0 мм. Принять коэффициент расхода такого отверстия равным μ = 0,62 и считать, что взаимное влияние ступеней дросселя отсутствует (скорость в промежутках между стенками гасится до нуля), а полная потеря напора распределяется между ступенями поровну. Определить полную потерю давления в дросселе при скорости течения в трубке v=1 м/с, если плотность жидкости р = 850 кг/м3.
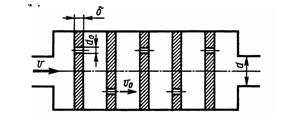
Ответ: ξ = 8130, ΔР = 3,5 МПа.
Скачать решение задачи 3.4 из Некрасова Б.Б (цена 70р)
Задача 3.5. Из резервуара, установленного на полу и заполненного жидкостью до высоты H, происходит истечение жидкости через отверстие в стенке. На какой высоте у должно быть отверстие, чтобы расстояние х до места падения струи на пол было максимальным? Определить это расстояние. Жидкость считать идеальной.
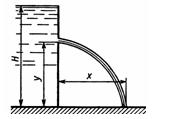
Ответ: у = 1/2Н, Х = Н.
Скачать решение задачи 3.5 из Некрасова Б.Б (цена 70р)
Задача 3.6. Жидкость вытекает через сопло диаметром d0, устроенное в горизонтальном дне сосуда. Найти связь между диаметром струи d и высотой z, если напор равен H. Сопротивлениями пренебречь.
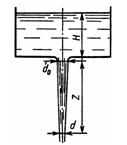
Скачать решение задачи 3.6 из Некрасова Б.Б (цена 70р)
Задача 3.7. При исследовании истечения через круглое отверстие диаметром d0 = 10 мм получено: диаметр струи dс = 8 мм; напор H = 2 м; время наполнения объема V = 10 л; t = 32,8 с. Определить коэффициенты сжатия ε, скорости φ, расхода μи сопротивления ξ. Распределение скоростей по сечению струи принять равномерным.
Ответ: ε = 0,64, φ = 0,97, μ = 0,62, ξ = 0,06.
Скачать решение задачи 3.7 из Некрасова Б.Б (цена 70р)
Задача 3.8. При истечении жидкости через отверстие диаметром d0 = 10мм измерены: расстояние х = 5,5 м (см. рис.), высота y = 4 м, напор H = 2 м и расход жидкости Q = 0,305 л/с. Подсчитать коэффициенты сжатия ε, скорости ф, расхода μ и сопротивления ξ. Распределение скоростей по сечению струи считать равномерным. Сопротивлением воздуха пренебречь.
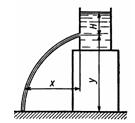
Ответ: ε = 0,638, φ = 0,972, μ = 0,62, ξ = 0,058.
Скачать решение задачи 3.8 из Некрасова Б.Б (цена 70р)
Задача 3.9. На рисунке показана схема устройства для исследования истечения через отверстия и насадки. Резервуар с жидкостью укреплен на двух опорах А и имеет возможность покачиваться в плоскости чертежа. При истечении из отверстия или насадка сила реакции струи выводит резервуар из положения равновесия, однако груз весом G возвращает его в это положение. Подсчитать коэффициенты сжатия струи е, скорости ф, расхода μ и сопротивления ξ при истечении воды, если известны размеры а = 1 м, b = 1 м, диаметр отверстия d0=10 мм. При опыте измерены: напор H = 2 м, расход Q = 0,305 л/с и вес груза G = 1,895 Н. Распределение скоростей в сечении струи принять равномерным.
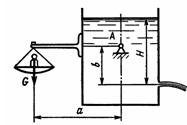
Ответ: ε = 0,621, φ = 0,998, μ = 0,62, ξ = 0,04.
Скачать решение задачи 3.9 из Некрасова Б.Б (цена 70р)
Задача 3.10. На рисунке изображена схема устройства, известного под названием «Геронов фонтан». Трубы А и Б заполнены водой, а труба В - воздухом. Объяснить принцип действия и определить скорость истечения воды из насадка (сопла) этого фонтана, если размеры H1 = 24 м, H2 = 4 м, H3 = 0,4 м. Потерями напора в системе и весом воздуха в трубе В пренебречь.
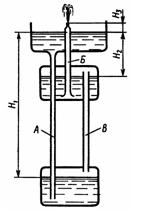
Ответ: v = 19,6 м/с.
Скачать решение задачи 3.10 из Некрасова Б.Б (цена 70р)
Задача 3.11. «Сосуд Мариотта» представляет собой плотно закрытый сосуд, в крышке которого укреплена трубка, сообщающая сосуд с атмосферой. Трубка может быть укреплена на различной высоте. В стенке сосуда имеется отверстие диаметром d0 = 10 мм, через которое происходит истечение в атмосферу. Какое давление установится в сосуде на уровне нижнего обреза трубки при истечении? Определить скорость истечения и время опорожнения «сосуда Мариотта» от верха до нижнего обреза трубки. Объемом жидкости в трубке и сопротивлением при истечении пренебречь (ε = 1). Форма сосуда цилиндрическая, D = 100 мм; H = 2 м, h1 = 0,2 м, h2 = 1 м.
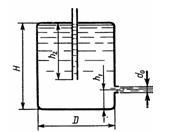
Ответ: Р = Ра, t = 25,2с.
Скачать решение задачи 3.11 из Некрасова Б.Б (цена 70р)
Задача 3.12. Как изменится расход воды Q (%) через внешний цилиндрический насадок (μ = 0,82) диаметром d0 = 20 мм, если к нему привинтить цилиндрическую трубку диаметром d = 30 мм и получить истечение с заполнением выходного сечения трубки? Потерей на трение по длине пренебречь. Подсчитать максимальный расход, при котором возможно такое истечение. Принять коэффициент сжатия струи внутри насадка ε = 0,64; hA = 750 мм рт. ст.; hнп = 40 мм рт. ст.
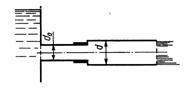
Ответ: ΔQ/Q0 = 30 %.
Скачать решение задачи 3.12 из Некрасова Б.Б (цена 70р)
Задача 3.13. Для сопла-заслонки, изображенной на схеме, определить силу, с которой жидкость воздействует на заслонку в следующих случаях: 1) когда заслонка плотно прижата к торцу сопла (x = 0) и истечения жидкости не происходит и 2) когда расстояние к достаточно велико и истечение происходит так, как показано на схеме. Давление в широкой части сопла (сечение 0-0) P0 = 3 МПа, скорость v0= 0 в обоих случаях. Диаметр выходного канала сопла d = 2 мм; а коэффициент расхода μ= φ = 0,85. Чему было бы равно отношение сил F2/F1 в двух случаях при отсутствии потерь напора в сопле? Указание. Во 2-м случае следует записать уравнение количества движения в направлении струи.
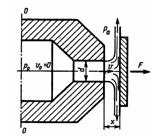
Ответ: F1 = 9,42 Н, F2 = 13,6 H, F2/F1 =2 (при φ = 1)
Скачать решение задачи 3.13 из Некрасова Б.Б (цена 70р)
Задача 3.14. Через жиклер, представляющий собой отверстие диаметром d0 = 2 мм в стенке толщиной б = 5 мм, происходит истечение жидкости в полость, заполненную той же жидкостью при избыточном давлении P2=1 МПа. Определить давление по другую сторону стенки P0, при котором внутри жиклера возникает кавитация. Давление насыщенных паров жидкости соответствует hнп = 60 мм рт. ст., р = 850 кг/м3. Коэффициент сжатия струи внутри жиклера принять равным ε = 0,64; коэффициент расхода, равный коэффициенту скорости, μ = φ = 0,82. Какой будет расход Q при начале кавитации? Указание. Следует записать уравнение Бернулли для сечений 1-1 и 2-2, при этом учесть потерю напора на внезапное расширение по теореме Борда и использовать уравнение расхода.
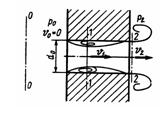
Ответ: Р0 = 2,31 МПа, Q = 0,143 л/с.
Скачать решение задачи 3.14 из Некрасова Б.Б (цена 70р)
Задача 3.15. Вода под избыточным давлением р1 = 0,3 МПа подается по трубе с площадью поперечного сечения S1=5 см2 к баллону Б, заполненному водой. На трубе перед баллоном установлен кран К с коэффициентом местного сопротивления 5. Из баллона Б вода вытекает в атмосферу через отверстие площадью S0=1 см2; коэффициент расхода отверстия равен μ = 0,63. Определить расход воды Указание. Записать уравнение Бернулли для сечений 1-1 и 2-2 и основную формулу для расхода при истечении.
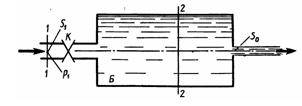
Ответ: Q = 1,49 л/с.
Скачать решение задачи 3.15 из Некрасова Б.Б (цена 70р)
Задача 3.16. Дан диффузорный насадок с плавно закругленным входом в виде сопла (ξс = 0,06) и диффузора с оптимальным углом конусности (α = 5°30/) и с соотношением диаметров D2/D1=3, для которого можно принять коэффициент сопротивления 0,125. Коэффициенты сопротивления отнесены к узкому сечению. Определить для данного насадка коэффициент расхода μ, отнесенный к площади выходного отверстия (D2), и коэффициент расхода μ', отнесенный к площади узкого сечения (D1).
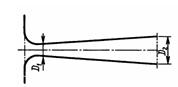
Ответ: μ = 0,25, μ/ = 2,25.
Скачать решение задачи 3.16 из Некрасова Б.Б (цена 70р)
Задача 3.17. Для выпуска воды из бака в его стенке устроено отверстие и введена труба, как показано на рисунке. Однако пропускная способность полученного насадка (внутреннего цилиндрического) оказалась недостаточной. Во сколько раз можно увеличить пропускную способность указанной трубы, не меняя ее диаметра и напора, если приставить к ней сопло (внутри бака) и диффузор снаружи? Трением внутри трубки пренебречь. Значения коэффициентов сопротивления сопла и диффузора, а также степень расширения диффузора взять из предыдущей задачи. Режим истечения в обоих случаях считать безотрывным и бескавитационным.
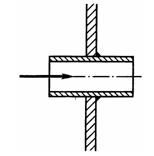
Ответ: Q/Q/ = 3,2
Скачать решение задачи 3.17 из Некрасова Б.Б (цена 70р)
Задача 3.18. Вода по трубе Т подается в резервуар A, откуда через сопло диаметром d1=8 мм перетекает в резервуар Б. Далее через внешний цилиндрический насадок d2= 10 мм вода попадает в резервуар В и, наконец, вытекает в атмосферу через внешний цилиндрический насадок d3 = 6 мм. При этом H =1,1 м; b = 25 мм. Определить расход воды через систему и перепады уровней h1 и h2. Коэффициенты истечения принять: μ1 = 0,97, μ2 = μ3 = 0,82.
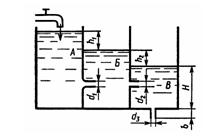
Ответ: Q = 0,109 л/с.
Скачать решение задачи 3.18 из Некрасова Б.Б (цена 70р)
Задача 3.19. При испытании модели гидротурбинного сопла диаметром d0=65 мм были произведены следующие измерения: давление воды в широкой части сопла (диаметром D=160 мм) P1 = 0,9 МПа; расход Q=96 л/с; диаметр струи dс = 55 мм. При помощи динамометра измерена сила воздействия струи на преграду F = 3,88 кН (диск установлен нормально к струе). Определить коэффициенты расхода и сопротивления двумя различными способами.
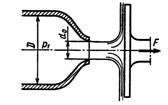
Ответ: μ = 0,678, ξ = 0,116.
Скачать решение задачи 3.19 из Некрасова Б.Б (цена 70р)
Задача 3.20. На рисунке показана упрощенная схема самолетного гидропневмоамортизатора. Процесс амортизации при посадке самолета происходит за счет проталкивания рабочей жидкости через отверстие d = 8 мм и за счет сжатия воздуха. Диаметр поршня D=100 мм. Определить скорость движения цилиндра относительно поршня в начальный момент амортизации, если первоначальное давление воздуха в верхней части амортизатора P1 = 0,2 МПа, расчетное усилие вдоль штока G = 50 кН, коэффициент расхода отверстия μ1 = 0,75, плотность рабочей жидкости р = 900 кг/м3.
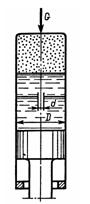
Ответ: v = 0,56 м/с.
Скачать решение задачи 3.20 из Некрасова Б.Б (цена 70р)
Задача 3.21. На рисунке изображена схема регулируемого игольчатого дросселя. Определить, на какое расстояние 1 необходимо вдвинуть иглу в дросселирующее отверстие для обеспечения перепада давления P = P1-P2 = 3 МПа, если угол иглы а = 30°, диаметр дросселирующего отверстия D = 6 мм, его коэффициент расхода м = 0,8, расход жидкости Q = 1,2 л/с, плотность рабочей жидкости р = 900 кг/м3. Указание. Площадь дросселирующего кольца определить по приближенной формуле S = S0 - SИ, где S0 - площадь отверстия, SИ - площадь иглы в сечении 1-1.
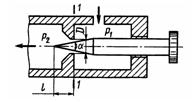
Ответ: L = 6,6 мм.
Скачать решение задачи 3.21 из Некрасова Б.Б (цена 70р)
Задача 3.22. Воздух под избыточным давлением Pо подается к пневмодатчику детали А. Проходя через пневмодроссель Д с проходным сечением (диаметром d=1 мм), затем через зазор, образуемый срезом сопла С и поверхностью детали A, воздух поступает в атмосферу. Определить, при каком зазоре х показание манометра М будет равно 0,5P0, если диаметр среза сопла d2=1,5 мм. Коэффициенты расхода через дроссель Д и зазор одинаковы. Считать воздух несжимаемым, его скорость в камерах В и K равна нулю.
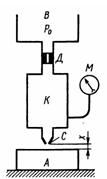
Ответ: х = 0,17 мм.
Скачать решение задачи 3.22 из Некрасова Б.Б (цена 70р)
Задача 3.23. Определить ширину проходного отверстия b и жесткость пружины с переливного клапана, который начинает перекрывать проходное отверстие при падении давления на входе рвх до 10 МПа и полностью перекрывает его при Pвх = 9 МПа. Перепад давления на агрегате P =Pвх-Рсист при полностью открытом золотнике и расходе Q= 1,5 л/с должен быть 0,3 МПа. Проходное отверстие выполнено в виде кольцевой щели, диаметр золотника D = 12 мм, коэффициент расхода окна золотника μ = 0,62; р = 850 кг/м3.
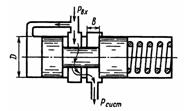
Ответ: спр = 46,7 Н/мм, b = 2,42 мм.
Скачать решение задачи 3.23 из Некрасова Б.Б (цена 70р)
Задача 3.24. Определить значение силы Р, преодолеваемой штоком гидроцилиндра при движении его против нагрузки со скоростью v= 20 мм/с. Давление на входе в дроссель Pн = 20 МПа; давление на сливе Pс = 0,3 МПа; коэффициент расхода дросселя μ = 0,62; диаметр отверстия дросселя d = 1,2 мм; D = 70 мм; dш = 30 мм; р = 900 кг/м3.
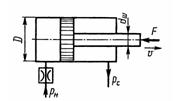
Ответ: F = 55 кН.
Скачать решение задачи 3.24 из Некрасова Б.Б (цена 70р)
Задача 3.25. Определить диаметр отверстия дросселя, установленного на сливе из гидроцилиндра, при условии движения штока цилиндра под действием внешней нагрузки F = 60 кН со скоростью v= 200 мм/с. Диаметры: штока dш= 40 мм, цилиндра D = 80 мм, коэффициент расхода дросселя м = 0,65, плотность жидкости р = 850 кг/м3, давление на сливе Pс = 0,3 МПа.
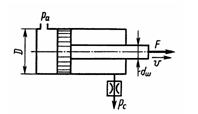
Ответ: d = 2,8 мм.
Скачать решение задачи 3.25 из Некрасова Б.Б (цена 70р)
Задача 3.26. Определить время полного хода поршня гидроцилиндра при движении против нагрузки, если давление на входе в дроссель рн = 16 МПа, давление на сливе Pс = 0,3 МПа. Нагрузка вдоль штока F = 35 кН, коэффициент расхода дросселя μ = 0,62, диаметр отверстия в дросселе dдр = 1 мм, плотность масла р = 900 кг/м3, диаметры: цилиндра D = 60 мм, штока d = 30 мм; ход штока L = 200 мм.
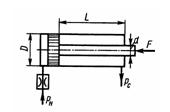
Ответ: t = 13,6 c.
Скачать решение задачи 3.26 из Некрасова Б.Б (цена 70р)
Задача 3.27. Жидкость с плотностью р = 850 кг/м3 подается от насоса в гидроцилиндр, а затем через отверстие в поршне площадью S0 = 5 мм2 и гидродроссель Д в бак (Рб = 0). 1) Определить, при какой площади проходного сечения дросселя Д поршень будет находиться в неподвижном равновесии под действием силы F = 3000 Н, если диаметр поршня D = 100 мм, диаметр штока dШ = 80 мм, коэффициент расхода отверстия в поршне μ0 = 0,8, коэффициент расхода дросселя μдр = 0,65, давление насоса Pн=1 МПа. 2) Определить площадь проходного сечения дросселя Д, при которой поршень будет перемещаться со скоростью vП=1 см/с вправо.
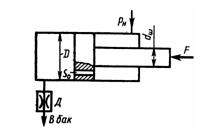
Ответ: 1) Sдр = 3,63 мм2; 2) Sдр = 0,74 мм2.
Скачать решение задачи 3.27 из Некрасова Б.Б (цена 70р)
Задача 3.28. Правая и левая полости цилиндра гидротормоза, имеющего диаметр поршня D =140 мм и диаметр штока dш = 60 мм, сообщаются между собой через дроссель с площадью проходного сечения Sдр = 20 мм2 и коэффициентом расхода μ = 0,65. Определить время, за которое поршень переместится на величину хода l = 350 мм под действием силы F = 15 кН, плотность жидкости р = 900 кг/м3.
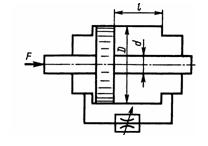
Ответ: t = 6,6 c.
Скачать решение задачи 3.28 из Некрасова Б.Б (цена 70р)
Задача 3.29. Изображенный на рисунке переливной клапан плунжерного типа предназначен для того, чтобы поддерживать заданное давление жидкости на входе P1 путем непрерывного ее слива. Однако точность поддержания давления зависит от размера клапана и характеристики пружины. Найти связь между расходом через клапан Q и давлением P1, если известны следующие величины: диаметр клапана d постоянное давление на выходе из клапана P2; сила пружины Fпр о при y = 0; жесткость пружины с, коэффициент расхода щелевого отверстия м, не зависящий от высоты подъема у. Можно считать, что давление р1 равномерно распределено по площади клапана π*d2/4. Задачу решить в общем виде. Указание. Следует записать выражение для расхода через коэффициент ц, площадь щели и перепад давления, а также уравнение равновесия клапана.
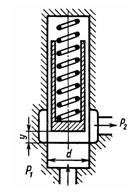
Скачать решение задачи 3.29 из Некрасова Б.Б (цена 70р)
Задача 3.30. Обратный клапан диаметром d= 20 мм служит для пропуска жидкости (р = 900 кг/м3) только в одном направлении. Определить перепад давления P = P1 – P2 на клапане, если P1 = 1,6 МПа. Жесткость пружины с = 13 Н/мм, ее предварительное поджатие y0 = 8 мм, максимальный ход клапана l = 3 мм, коэффициент расхода μ = 0,8, объемный расход Q = 1 л/с.
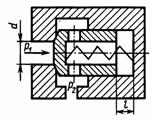
Ответ: ΔР = 0,46 МПа.
Скачать решение задачи 3.30 из Некрасова Б.Б (цена 70р)
3 Истечение жидкости через отверстия, насадки, дроссели и клапаны часть 2
Задача 3.31. Редукционный клапан предназначен для обеспечения постоянного давления на выходе из него P2 = 11 МПа. Определить требуемые жесткость пружины и ее предварительное поджатие (при полностью открытом клапане), обеспечивающие изменение давления за клапаном ΔP2 = ±4%*P2, если его диаметр d=12 мм, максимальный ход t = 3 мм, угол конуса а = 60°, коэффициент расхода дросселирующей щели А м = 0,8, плотность рабочей жидкости р = 900 кг/м3. Каков максимальный расход жидкости через клапан, если максимальное давление перед ним р1 = 12 МПа? Указание. Площадь проходного сечения конусной щели А определить по упрощенной формуле Sщ = π*d*h*sin (α/2), где h - ход клапана.
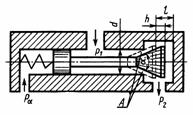
Ответ: с = 33 Н/мм, h0 = 36 мм, Q = 2,56 л/с.
Скачать решение задачи 3.31 из Некрасова Б.Б (цена 70р)
Задача 3.32. Считая жидкость несжимаемой, определить скорость движения поршня под действием силы F= 10 кН на штоке, диаметр поршня D = 80 мм, диаметр штока d = 30 мм, проходное сечение дросселя Sдр = 2 мм2, его коэффициент расхода μ = 0,75, избыточное давление слива Рс = 0, плотность рабочей жидкости р=900 кг/м3.
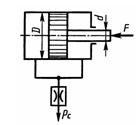
Ответ: vn = 0,376 м/с
Скачать решение задачи 3.32 из Некрасова Б.Б (цена 70р)
Задача 3.33. Определить перепад давления ΔР = P1-P2 в системе гидропривода за дросселирующим распределителем при перемещении его золотника на х = 2 мм, если подача насоса равна расходу на сливе: Qн = Qс=1 л/с; давление насоса Pн = 5 МПа; давление слива Pс = 0,2 МПа; коэффициенты расхода дросселирующих щелей μ = 0,75; диаметр золотника распределителя d=12 мм, плотность рабочей жидкости р = 900 кг/м3.
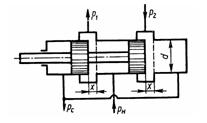
Ответ: ΔР = 4,52 МПа.
Скачать решение задачи 3.33 из Некрасова Б.Б (цена 70р)
Задача 3.34. На рисунке представлена конструктивная схема регулятора расхода (клапан, обеспечивающий постоянство расхода). Он состоит из корпуса 1 с дросселирующими отверстиями 4, подвижного плунжера 3 с дросселирующим отверстием 2 и пружины 5. Определить, при каком значении силы пружины Fпр регулятор будет обеспечивать расход Q = 5 л/мин, если диаметры D = 20 мм, d = 3 мм; коэффициенты расхода дросселирующих отверстий μ = 0,8; плотность рабочей жидкости р = 900 кг/м3. Считать, что в пределах рабочего хода плунжера сила пружины остается постоянной.
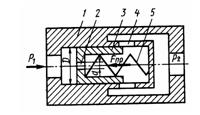
Ответ: Fnp = 30,7 МH.
Скачать решение задачи 3.34 из Некрасова Б.Б (цена 70р)
Задача 3.35. На рисунке показан гидроаппарат, назначение которого заключается в том, что в случае разрушения трубопровода 1 клапан 3 перекрывает отверстие 2 и тем самым препятствует выбросу рабочей жидкости из гидросистемы. При нормальной работе перепад давления в полостях а и 6, обусловленный сопротивлением отверстий 4, недостаточен для сжатия пружины 5 и клапан 2 под действием силы предварительного поджатия пружины F0 = 200 Н находится в крайнем правом положении. Определить минимальное значение расхода Q, при котором клапан 3 начнет перемещаться влево, если известно: D = 20 мм; суммарная площадь отверстий 4 S0 = 0,5 см2; коэффициент расхода отверстий μ = 0,62; плотность жидкости р = 900 кг/м3. Выразить в общем виде силу, с которой клапан 3 будет прижиматься к седлу в случае разрушения трубопровода 1, приняв: максимальный ход клапана х, жесткость пружины с, диаметр отверстия 2 d, давление на входе в гидроаппарат Pн.
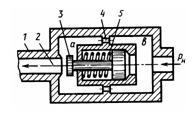
Ответ: Q = 70 л/мин.
Скачать решение задачи 3.35 из Некрасова Б.Б (цена 70р)
Задача 3.36. Определить расход бензина через жиклер Ж карбюратора диаметром d=1,2 мм, если коэффициент расхода жиклера μ = 0,8. Сопротивлением бензотрубки пренебречь. Давление в поплавковой камере атмосферное. Дано разрежение (вакуум) в горловине диффузора Pвак = 18 кПа, рб = 750 кг/м3.
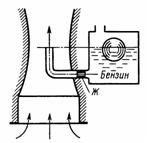
Ответ: Q = 22,6 л/ч.
Скачать решение задачи 3.36 из Некрасова Б.Б (цена 70р)
Задача 3.37. На рисунке показан простейший карбюратор двигателя внутреннего сгорания. Поток воздуха, засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (обрез трубки). Скорость воздуха в этом сечении возрастает, а давление падает. Благодаря этому бензин подсасывается из поплавковой камеры и вытекает через распылитель, смешиваясь с потоком воздуха. Найти соотношение между массовыми расходами воздуха и бензина Qвоз/Qб, если известны: размеры D = 30 мм; dж = 1,8 мм; коэффициент сопротивления воздушного канала до сечения 2-2 ξв = 0,05; коэффициент расхода жиклера μ = 0,8. Сопротивлением бензотрубки пренебречь. Плотности: воздуха рвоз=1,25 кг/м3; бензина рб = 750 кг/м3.
Указание. Следует записать уравнение Бернулли для воздушного потока (сечение 0-0 и 2-2) и уравнение истечения для бензина. При этом учесть, что давления бензина и воздуха в сечении 2-2 одинаковы.
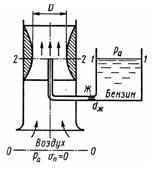
Ответ: Qв/Qб = 14,8.
Скачать решение задачи 3.37 из Некрасова Б.Б (цена 70р)
Задача 3.38. К поршню ускорительного насоса карбюратора диаметром D=16 мм приложена сила F = 5 Н. Вследствие этого бензин движется по каналу диаметром d = 2 мм через клапан K, а затем через жиклер диаметром dж = 0,8 мм вытекает в воздушный поток. Определить расход бензина, приняв следующие коэффициенты: сопротивления клапана 10 (отнесено к dж), расхода жиклера μж = 0,8 (отнесено к dж). Давления воздуха над поршнем и в воздушном потоке одинаковы. Сопротивлением канала (диаметром d) пренебречь, плотность бензина р = 750 кг/м3.
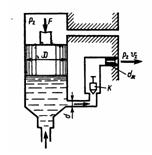
Ответ: Q = 10,6 л/ч
Скачать решение задачи 3.38 из Некрасова Б.Б (цена 70р)
Задача 3.39. Даны разрежение в горловине диффузора карбюратора Pвак= 10 кПа и диаметры жиклеров: экономического dЖ1 = 1 мм и главного dЖ2 = 0,8 мм. Определить расход бензина через главную дозирующую систему, считая коэффициенты расхода жиклеров одинаковыми: μ = 0,8; рб = 700 кг/м3; h = 0.
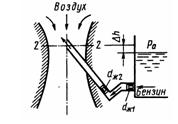
Ответ: Q = 6,5 л/ч.
Скачать решение задачи 3.39 из Некрасова Б.Б (цена 70р)
Задача 3.40. На рисунке изображена схема автомобильного карбюратора, которая обеспечивает обеднение смеси при большом разрежении в диффузоре 1 за счет того, что в распылитель 2 кроме топлива через основной дозирующий жиклер 4 будет поступать воздух через трубку 3. Определить максимальный расход топлива Q без подсоса воздуха в распылитель, если высота жидкости в поплавковой камере h = 20 мм; диаметр жиклера 4 dж = 3 мм; коэффициент расхода μ = 0,8.
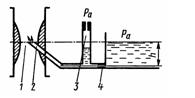
Ответ: Q = 12,8 л/ч.
Скачать решение задачи 3.40 из Некрасова Б.Б (цена 70р)
Задача 3.41. На рисунке изображена система карбюратора двигателя внутреннего сгорания с ускорительным насосом для мгновенного обогащения топливной смеси. При резком открытии дроссельной заслонки 1 поршень 2 ускорительного насоса движется вниз. Под действием давления, возникшего под поршнем, открывается клапан 3 (клапан 4 закрыт) и топливо подается в диффузор карбюратора дополнительно, помимо основной дозирующей системы, состоящей из жиклера 5 и распылителя 6. Определить, во сколько раз увеличится подача топлива в диффузор, если в его горловине давление Pвак = 0,02 МПа; расход топлива через основную дозирующую систему Q = 8 см3/с; диаметр трубопровода ускорительного насоса 4 dж = 2 мм; коэффициент расхода клапана Pж = 0,78; проходное сечение клапана SК = 0,4 мм2; скорость движения поршня ускорительного насоса V = 0,1 м/с; диаметр поршня D = 10 мм; высота h = 20 мм; радиальный зазор между поршнем и цилиндром б = 0,1 мм; вязкость топлива v = 0,01 Ст, его плотность р = 800 кг/м3. Потерями напора в трубопроводах пренебречь. Учесть утечки через щелевой зазор между поршнем и цилиндром, считая их соосными.
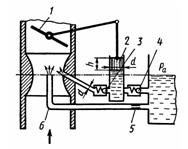
Ответ: Qв/Q = 1,44.
Скачать решение задачи 3.41 из Некрасова Б.Б (цена 70р)
Задача 3.42. Воздух плотностью рв=1,28 кг/м3 всасывается двигателем через фильтр 1 с коэффициентом сопротивления ξФ = 3 (отнесен к d1), затем по трубе диаметром d1 = 50 мм попадает в диффузор 2 карбюратора, сопло которого имеет коэффициент сопротивления ξс = 0,1 (отнесен к d2). В узком сечении диффузора диаметром d2 = 30 мм расположено выходное отверстие распылителя 3. Благодаря разрежению, возникающему в горловине диффузора, бензин с плотностью рб = 790 кг/м3 подсасывается из поплавковой камеры 4 и через жиклер 5 с коэффициентом расхода м= 0,6 и распылитель попадает в воздушный поток. Свободная поверхность бензина в поплавковой камере находится ниже выходного отверстия распылителя на высоту h=10 мм. Определить диаметр отверстия жиклера д, для обеспечения коэффициента избытка воздуха а=1, если a=Qв/(14,8*Qб) где Qв - массовый расход воздуха; Qб = 15,0 кг/ч - массовый расход бензина. Гидравлическими потерями трубки распылителя пренебречь.
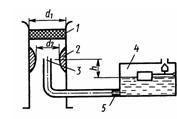
Ответ: dж = 1,8 мм.
Скачать решение задачи 3.42 из Некрасова Б.Б (цена 70р)
Задача 3.43. Определить время полного опорожнения цилиндрического бака, заполненного жидкостью. Площадь основания бака S=1 м2 и высота Н=1 м. Истечение происходит в атмосферу через отверстие в дне бака с закругленными кромками (сопло) диаметром d1 = 10 мм.
Задачу решить, если:
1) бак открыт и давление воздуха на поверхности жидкости атмосферное;
2) бак закрыт, но в крышке имеется отверстие диаметром d2 = 3 мм.
Воздух при опорожнении бака всасывается через это отверстие внутрь и над поверхностью жидкости создается разрежение.
Коэффициент расхода отверстий принять μ=1.
Указание. В обоих случаях записать равенство между объемом жидкости, вытекшей за время dt, и уменьшением объема жидкости в баке (снижение уровня на dh). Во втором случае, кроме того, следует записать уравнение расхода для потока воздуха. Затем в обоих случаях следует выполнить интегрирование в пределах от h = Н до h = 0. Воздух считать несжимаемым, плотность рвоз = 1,3 кг/м3.
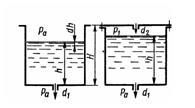
Ответ: 1) t = 1,6 ч; 2) t = 1,72 ч.
Скачать решение задачи 3.43 из Некрасова Б.Б (цена 70р)
Задача 3.44. Сравнить времена опорожнения одинаковых конических сосудов с углом конуса L, и высотой hо, один из которых расположен вершиной вверх (а), а другой - вершиной вниз (б). В обоих случаях истечение происходит через отверстие диаметром d0 с коэффициентом расхода м. Давление на свободной поверхности жидкости считать атмосферным, а течение - установившимся. Принять, что h0>>d0.
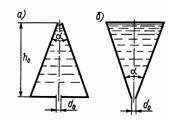
Ответ: t1/t2 = 8/3.
Скачать решение задачи 3.44 из Некрасова Б.Б (цена 70р)
Задача 3.45. Определить время опорожнения бака прямоугольного сечения через внешний цилиндрический насадок, устроенный в дне:
1) при постоянном значении коэффициента расхода μ0 = 0,81, что соответствует числам Рейнольдса, большим предельного, т. е. Rе>Rепр, где Rе = d*(2*g*H)0,5/v, а Rепр = 105; 2) с учетом зависимости коэффициента расхода от числа Рейнольдса при Rе<Rепр, имеющей вид μ = А*Rеm, где m = 0,1 и A = 0,256. Длиной насадка пренебречь.
Размеры бака 0,5*1,2 м; диаметр отверстия насадка d = 50 мм; начальный напор (максимальный) H0 = 0,5 м; кинематическая вязкость жидкости v = 0,01 см2/с.
Указание Интегрирование исходного дифференциального уравнения во втором случае провести сначала для промежутка времени от t = 0 (H = H0) до t = tпр (H = Hпр) при м = const, затем для H<Hкр при условии μ = var от t = tпр до t = tк (H=0). (Индекс «пр» означает предельное значение параметра, соответствующее предельному числу Рейнольдса.)
Скачать решение задачи 3.45 из Некрасова Б.Б (цена 200р)
Задача 3.46. В напорную линию системы смазки двигателя внутреннего сгорания включена центрифуга, выполняющая роль фильтра тонкой очистки масла от абразивных и металлических частиц. Ротор центрифуги выполнен в виде полого цилиндра, к которому подводится масло под давлением Pо = 0,5 МПа, как показано на схеме, а отводится через полую ось, снабженную отверстиями. Часть подводимого масла вытекает через два сопла, расположенные тангенциально так (А-A), что струи масла создают реактивный момент, вращающий ротор. Определить скорость истечения масла через сопла (относительно ротора) и реактивный момент при частоте вращения ротора n=7000 об/мин. Диаметр отверстий сопл d0 = 2,5 мм; μ = ф = 0,65; расстояние от оси отверстий до оси вращения ротора R = 60 мм; рм = 900 кг/м3. Считать, что в роторе масло вращается с той же угловой скоростью, что и ротор.
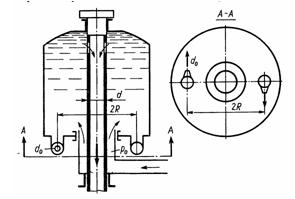
Задача 3.47. На рисунке показана схема автомобильного гидроамортизатора двойного действия. При плавном движении поршня 1 вниз (ход сжатия) жидкость из-под поршня перетекает в пространство над поршнем через отверстия 2 и 7, а через отверстия 4 закрытого клапана 5 в компенсационную кольцевую полость 6, в верхней части которой воздух сжимается.
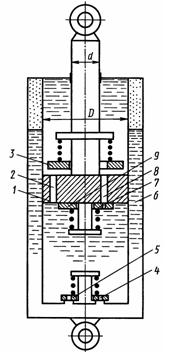
При обратном плавном движении поршня 1 вверх (ход отбоя) жидкость перетекает в нижнюю полость через отверстия 7 и 8. Кроме того, часть жидкости возвращается из компенсационной полости через открывающийся при этом клапан 5. При резком отбое перетекание жидкости обеспечивается еще открытием клапана 9 (при резком ходе сжатия открывается клапан, который на схеме не показан). Так как пружины клапанов 3 и 5 являются слабыми, а каналы достаточно велики, то сопротивление этих клапанов пренебрежимо мало. Поэтому основным сопротивлением потоку жидкости при ходе сжатия являются калиброванные отверстия 4 в клапане 5, а при ходе отбоя - калиброванные отверстия 7 в клапане 9. Определить скорости перемещения поршня относительно цилиндра при плавном ходе сжатия (VI) и плавном ходе отбоя (02), если значение силы вдоль штока F = 400 Н, которая направлена в первом случае вниз, а во втором - вверх. Диаметры: поршня D= 40 мм, штока d=16 мм. Площадь отверстий 7 S1 = 1,0 мм2; площадь отверстий 4 S2 = 0,2 мм2. Коэффициенты расхода отверстий принять одинаковыми μ = 0,60. Давление воздуха в полости 6 не учитывать, р = 850 кг/м3.
Указание. Ввиду малости сопротивлений клапанов 3 и 5 считать при ходе сжатия давления жидкости по обе стороны поршня одинаковыми, а при ходе отбоя давление под поршнем принять за атмосферное. Для обоих случаев записать уравнение равновесия поршня и уравнение истечения.
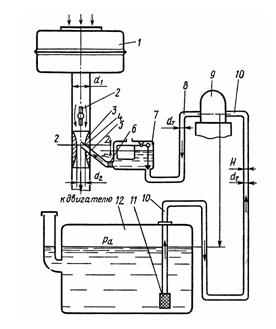
Задача 3.48. Воздух засасывается двигателем из атмосферы, проходит через воздушный фильтр 1 (ξ1) и затем по трубе диаметром d1 минуя дроссельную заслонку 2 (ξ2) подается в диффузор 4 карбюратора, сопло 3 которого имеет коэффициент сопротивления ξ3. В узком сечении 2-2 диффузора расположено выходное отверстие распылителя 5. Бензин засасывается из бака 12 через сетчатый фильтр 11 с коэффициентом сопротивления ?ф на высоту Н по всасывающему трубопроводу 10 диаметром йт и длиной l насосом 9 и по трубопроводу 8 подается в поплавковую камеру карбюратора 7. Все колена (повороты) в трубопроводе считать одинаковыми; коэффициенты сопротивления ? к. Благодаря разрежению, возникающему в горловине диффузора 4, бензин подсасывается из поплавковой камеры карбюратора 7, проходит через жиклер 6 с коэффициентом расхода м и вытекает в воздушный поток через распылитель 5.
Определить: абсолютное давление бензина перед входом в насос; диаметр жиклера. Имеем следующие данные: ξ1=3; ξ2=1; ξ3 = 0,1; ξk = 0,8; ξф=6, μ=0,75, d1=50мм, d2=35 мм, dт=5мм, H=5м, h= 0; l = 5 м; hа = 750 мм рт. ст.; Pб = 750 кг/м3; = 0,01 см2/с; Pв=1,28 кг/м3; а=1; рб=150 Н/ч.
Следует учесть: коэффициент избытка воздуха а =Qв/14Qб; коэффициенты ξ1 и ξ2 отнесены к диаметру , d1, ξ3 - к d2, а ξk и ξф - к dт; сопротивлением трубки распылителя пренебречь.
Указание. Для определения диаметра жиклера необходимо составить уравнение Бернулли для потока воздуха и уравнение истечения бензина через жиклер.
Скачать решение задачи 3.48 из Некрасова Б.Б (цена 200р)
Cтраница 1 из 2


